Prof. Túlio Jorge dos Santos (25/04/2007)







O astrônomo Eratóstenes ficou muito conhecido por ter calculado o perímetro da Terra (e consequentemente seu raio) com uma precisão surpreendente para a época, 235 AC, e por utilizar um método científico consistente para tal fim.
Seu método consistiu no seguinte: o sábio ficou sabendo que no solstício de verão (dia mais longo – noite mais curta) no dia 21 de junho um gnomon (um estilete vertical fincado no solo na direção perpendicular) não apresentava sombra na cidade de Siena (hoje Asuam – vide mapa), mas na cidade de Alexandria um estilete nas mesmas condições apresentava uma sombra. Ele atribuiu este fato à esfericidade da Terra. Conta a “história” que Eratóstenes mandou um escravo a pé, medir a distância entre as duas cidades.
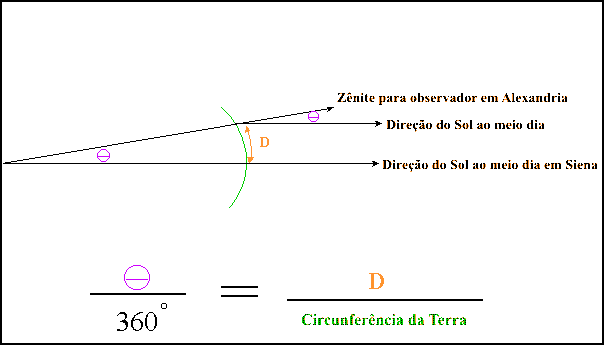
Ele então mediu, no mesmo dia 21 de junho, o comprimento da sombra em Alexandria verificando um ângulo de θ = 7,5° ao sul do zênite. Com a simples proporção de que a circunferência da Terra está para a distância entre as duas cidades assim como o ângulo da circunferência (360°) está para o ângulo medido ele pode determinar a circunferência da Terra (vide figura). A distância nesta época era medida em estádios e Eratóstenes computou 252.520 estádios, o equivalente a 40.000 km. O que resultou para o raio da Terra aproximadamente 6.400 km. O valor hoje é cerca de 6,378 km. Seus cálculos foram apresentados na sua obra “Sobre a medida da Terra” que infelizmente se perdeu. Mas são citados por Cleomedes, Theon de Smyrna e Strabo.

Vamos descrever dois métodos para estimar a distância entre a Terra e a Lua.
Consta que o grego Aristarco, por volta de 250 AC, foi o primeiro a estimar a diâmetro da Lua através da observação de um eclipse lunar total. A geometria de um eclipse lunar está representada na figura abaixo [2].
Considere o momento em que a Lua penetra a sombra da Terra. Vide figura abaixo.

Aqui, D = 2RT é o diâmetro da Terra e o segmento OQ = DTL é a distância Terra – Lua. No triângulo OPQ temos:
Para determinarmos o valor de θ, basta lembrar que a Lua percorre um ângulo de 360° em um mês lunar que vale 27,322 dias aproximadamente. Vide figura ao lado.
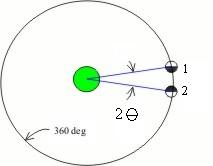
Nestas condições a razão entre o tempo transcorrido para completar o arco de círculo 2q, da posição 1 à posição 2, e o tempo para dar uma volta completa em torno da Terra é equivalente à razão entre o ângulo e 360°, isto é,
T12 / 27,322dias = 2 θ/ 360°.
Onde T12 é o tempo medido desde metade da lua obscurecida no início do eclipse até que sua metade apareça iluminada ao sair da sombra da Terra e 29.5 dias é o tempo médio entre duas lunações (mês lunar). Assim,
θ (graus) = ½ 360 (T12 / 27.332dias)
.Para obter o valor de θ basta medir o tempo transcorrido desde o momento que metade da Lua está coberta no início do eclipse até o momento em que metade dela está iluminada saindo do eclipse. A figura abaixo mostra a seqüência de um eclipse lunar total.
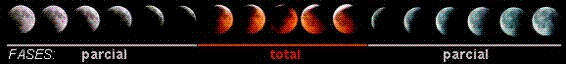
Uma vez conhecido o ângulo θ e conhecendo o raio da Terra pode-se por fim calcular a distância Terra-Lua.
Procure identificar as fontes de erro presentes no procedimento.
O segundo método utiliza a medida direta do tamanho angular da Lua. O tamanho angular médio da Lua no céu é de 0,5°. Considerando na figura abaixo, R sendo o diâmetro da Lua, D a distância Terra-Lua e a metade do tamanho angular da Lua:
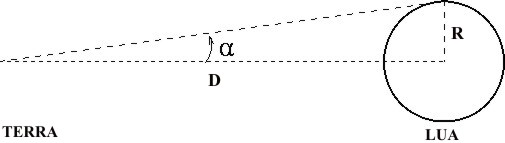
A distância D será dada por:
Aristarco também calculou a distância Terra-Sol. Ele estimou o valor do ângulo subentendido entre a direção Terra-Lua (a, na figura abaixo) que é a separação angular Sol-Lua. Ele assumiu ainda, que no quarto crescente (ou minguante) o ângulo entre a direção Terra-Lua e a direção Lua-Sol é reto (vale 90°)
.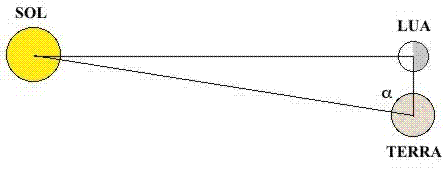
Uma simples relação trigonométrica dá:
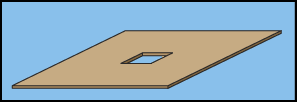
cos α = distância Terra-Lua / distância Terra-Sol Aristarco estimou α ~ 87° o que levou a um resultado muito menor que o medido atualmente. Isto se deveu ao instrumento pouco preciso disponível na época. Mas, o procedimento é correto. O valor atual aceito é α ~ 89.853°, com isto a distância Terra-Sol é cerca de 149,670,772 km.Para calcularmos o diâmetro do Sol vamos utilizar a projeção por “pinhole”. Um projetor “pinhole” pode ser construído utilizando um pedaço de papelão, papel alumínio, fita adesiva e uma agulha de costura. Proceda da seguinte maneira [3]
:
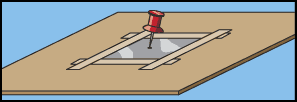
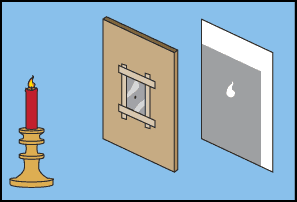
Observe o que acontece com o tamanho da imagem quando o anteparo se distancia do projetor. O que acontece quando a vela se distancia?[4]
O diagrama [5] abaixo ilustra a projeção da imagem do sol por um orifício sobre anteparo horizontal.

Assim, num dia ensolarado, podemos estimar o diâmetro do Sol medindo h, distância do orifício ao anteparo horizontal e d, tamanho da imagem, por:
D = 150,000,000 d/h km
O mesmo procedimento pode ser usado para estimar o diâmetro da Lua numa noite de Lua cheia.
O astrolábio é um antigo instrumento utilizado pelos astrônomos para determinar posições dos astros no céu. Consta que foi inventado na Grécia por Hiparco no século II AC ou pelo matemático Apolônio de Perga no século III AC. Consta também, que foi introduzido pelos árabes na Europa no século X.
Para construir um, você vai precisar de um pedaço de papelão, cola, tesoura, fita adesiva, um canudo de plástico, linha e uma argola de metal ou um outro “peso”.
Antes de qualquer coisa imprima o desenho do Astrolábio que se encontra no Anexo.
Cole o desenho do astrolábio sobre o papelão e recorte. Faça um orifício na posição indicada no desenho. Prenda o canudo na direção indicada. Use a linha e o “peso” pendente do orifício para obter um marcador. A seqüência de figuras abaixo ilustra o procedimento de construção do instrumento.
Para se familiarizar com o uso do astrolábio, meça altitudes (alturas angulares) de árvores e prédios. Mire através do canudo para o topo da árvore ou do prédio e peça alguém para fazer a leitura do valor do ângulo onde a linha cruza a escala. A figura abaixo ilustra o procedimento.

Desta maneira é possível determinar altitudes da Lua, de planetas e estrelas.
Para observações de altitudes do Sol devemos sempre lembrar: nunca olhe diretamente para o Sol!!! Risco de lesão permanente na retina!!! Mova o astrolábio em direção ao Sol até ver na palma da outra mão a sombra do canudo. Continue movendo suavemente até obter um círculo luminoso focalizado na palma da mão. Aí o astrolábio estará apontado diretamente para o Sol. Peça alguém para anotar a leitura na escala. Anote a data e a hora da observação. Uma vez por semana no mesmo horário meça a altitude do Sol com o astrolábio. Registre suas observações numa tabela não se esquecendo de anotar a data e a hora da observação. Analisando suas observações procure ver se há uma variação na altitude. A altitude está aumentando ou diminuindo? Estas variações são diferentes nas diferentes épocas do ano? Procure entender os resultados em termos do ângulo de inclinação da Terra.
A representação em escala do Sistema Solar é uma ferramenta excepcional para ilustrar distâncias e tamanhos que caracterizam a vastidão do universo. Daí sua importância como instrumento educacional.
A distância Terra-Sol é aproximadamente 150,000,000 km, o que define uma Unidade Astronômica (UA). O fator de escala 1/10,000,000 para a distância e 5,0 cm para o diâmetro da Terra produz a tabela abaixo:
| Tamanho (cm) | Distância do Sol (m) | Tempo de viagem da luz | Tempo de viagem | |
|---|---|---|---|---|
| Mercúrio | 2.0 | 5.8 | 3.2 min | 5 meses |
| Vênus | 5.0 | 10.8 | 6.0 min | 3 meses |
| Terra | 5.0 | 15.0 | 8.3 min | - |
| Marte | 2.5 | 22.8 | 12.7 min | 8 meses |
| Júpiter | 56.5 | 77.8 | 43,0 min | 1.5 anos |
| Saturno | 20.5 | 142.9 | 1.3 h | 3.2 anos |
| Urano | 20.5 | 287.1 | 2.7 h | 8.5 anos |
| Netuno | 19.5 | 450.4 | 4.2 h | 12.0 anos |
Nesta escala de o diâmetro da Terra que é 12,740 km, vale 5.0 cm. O diâmetro do Sol que é aproximadamente um pouco mais 100 vezes o diâmetro da Terra e vale 1,400,000 km, nesta escala terá um diâmetro de quase 550 cm. A Lua tem a dimensão de 1.4 cm e se encontra a um pouco menos de 4,0 cm da Terra. O Sistema Terra-Lua cabe na palma da mão e é bom lembrar que a distância à Lua é a distância máxima que o homem viajou até hoje. Nesta escala o planeta anão Plutão está a uma distância de quase 600 m.
Também nesta escala a velocidade da luz é de 3.0 cm/s o que equivale aproximadamente à velocidade de deslocamento de uma mosca.
Um visitante pode percorrer a distância compreendida pelo modelo caminhando por cerca de 10 minutos; cada passo representa aproximadamente 10,000,000 km. A nave Voyager 2 – que visitou Júpiter em 1979, Saturno em 1981, Urano em 1986 e Netuno em 1989 – gastou uma década para percorrer a mesma distância.
Para termos uma apreciação do tamanho do universo considere o seguinte: a estrela mais próxima (chamada Próxima Centauro) será localizada a cerca de 4,000 km além, o que corresponde aproximadamente à distância Belo Horizonte-Recife. Esta distância é quase 30,000 vezes menor que o diâmetro da Via Láctea.
Nesta escala 1 Angstrom = 1 m e 1 al = 1,000 km.
Diagrama do Astrolábio
[1]Adaptado de Antonio Fernandes Neto – Crianças e estrelas – Editora Bloch - 1979
[2] Adaptado de Hermit Eclipse
[3] Fonte: CSE – UC Berkeley
[4]A expressão s = Ö 2 x 1.22 lh relaciona o diâmetro do orifício s, o comprimento de onda, que para o Sol vale l=5,000 Angstroms, e h, distância do orifício à imagem.
[5] Adaptado de Royal Astronomical Society of Canada - PGC
[6] Idem (3)