Prof. Túlio Jorge dos Santos (16/08/2007)
Apresentamos uma versão do experimento de Herschel que conduziu à descoberta de uma radiação invisível (o infravermelho) em 1800[1].
Introdução: A luz do Sol ao passar por um prisma de vidro sofre uma dispersão apresentando um espectro mostrando as cores do arco íris. O espectro da luz Solar contém todas as cores visíveis ao olho humano. Herschel mediu temperaturas nas cores do espectro solar e observou um aumento da temperatura do azul ao vermelho. Ao colocar um termômetro além da parte vermelha do espectro, onde não havia luz visível, ele observou uma temperatura ainda mais alta que as outras. Herschel descobriu então um novo tipo de luz, invisível aos olhos humanos. Este tipo de luz ficou conhecido como infravermelho. Infra em latim significa além.
Parte experimental
Material utilizado: Prisma de vidro, três termômetros e caixa de papelão.
Montagem: vide figura abaixo.
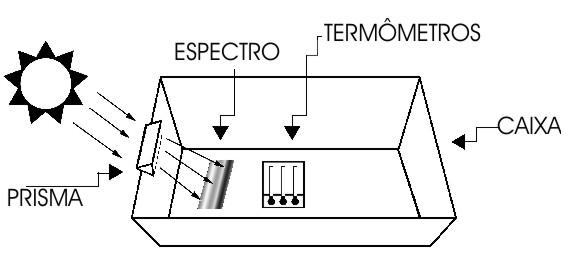
Procedimento: Prenda o prisma no topo de um dos lados da caixa, coloque os termômetros sobre um suporte de maneira a estarem dispostos em distâncias suficientes para cobrir os intervalos de cores indicadas e para a região fora do espectro (as escalas devem estar alinhadas), conforme indicado na figura abaixo. De forma a obter uma maior precisão nas medidas de temperaturas é aconselhável escurecer os bulbos dos termômetros para que possam absorver melhor o calor.
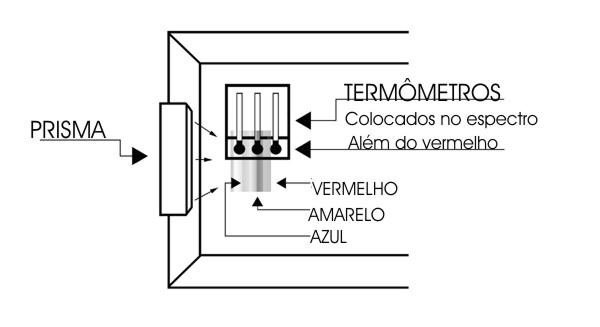
Em um dia ensolarado leve a montagem para o ar livre, a presença de nuvens diminui o efeito do prisma, incline ligeiramente a caixa para obter um espectro bem estendido. Coloque inicialmente os termômetros na sombra e anote a temperatura ambiente do ar. Então os disponha como indicado anteriormente. O tempo necessário para que os termômetros atinjam valores finais é de cerca de 5 minutos. Anote nos quadros abaixo as temperaturas observadas.
| Termômetro 1 | Termômetro 2 | Termômetro 3 | |
|---|---|---|---|
| Temperatura à sombra |
| Temperatura no espectro | Termômetro 1 (azul) | Termômetro 2 (vermelho) | Termômetro 3 (infravermelho) |
|---|---|---|---|
| Após 1 minuto | |||
| Após 2 minutos | |||
| Após 3 minutos | |||
| Após 4 minutos | |||
| Após 5 minutos |
Calcule as diferenças entre as temperaturas finais medidas no espectro e as temperaturas medidas na sombra pelos três termômetros.
| Termômetro 1 | Termômetro 2 | Termômetro 3 | |
|---|---|---|---|
| Tespectro | |||
| Tsombra | |||
| Tespectro-Tsombra/td> |
Calcule as diferenças entre as temperaturas finais em cada parte do espectro.
| Termômetro 1 | Termômetro 2 | Termômetro 3 | |
|---|---|---|---|
| Tespectro |
Calcule as temperaturas médias em cada parte do espectro
| Soma das Temperaturas | Número de observações | Temperatura média | |
|---|---|---|---|
| Amarelo | |||
| Azul | |||
| Infravermelho |
Calcule as diferenças médias entre as temperaturas finais em cada parte do espectro e as temperaturas na sombra para os três termômetros.
| Soma das Temperaturas | Número de observações | Temperatura média | |
|---|---|---|---|
| Amarelo | |||
| Azul | |||
| Infravermelho |
Calcule as diferenças médias entre as temperaturas finais em cada parte do espectro e as temperaturas na sombra para os três termômetros.
| Soma das diferenças de temperatura | Número de observações | Média | |
|---|---|---|---|
| Tamarelo-Tazul | |||
| Azul | |||
| Infravermelho |
Questões: O que você notou acerca das leituras de temperatura? Você notou alguma tendência?Qual foi o valor mais alto da temperatura lida? O que você acha que existe além do vermelho?
Um procedimento parecido levou o cientista alemão Johann Ritter à descoberta da radiação ultravioleta no ano seguinte.
Uma das mais notáveis propriedades do universo pode ser resumida na seguinte frase:
“Quanto mais distante vemos um objeto mais no passado estamos observando-o”.
O Sol se encontra a uma distância de cerca de 150,000,000 de quilômetros. A velocidade da luz é 300,000 km/s. Uma simples operação revela que a luz do Sol leva cerca de 8 minutos para chegar até nós. Assim sendo, estamos recebendo a radiação solar emitida oito minutos atrás. A estrela mais próxima de nós (Próxima Centauro) se encontra a aproximadamente 4.2 anos luz, isto é, a luz desta estrela que chega até aqui foi emitida a 4.2 anos atrás.
Em relação aos astros, duas características se destacam: a luminosidade intrínseca e o brilho aparente.
A luminosidade intrínseca é a quantidade de energia emitida pelo astro na unidade de tempo. É independente da distância.
O brilho aparente, por sua vez está relacionado a ela através da “Lei do inverso do quadrado da distância” e é diretamente proporcional à luminosidade intrínseca. Sendo d a distância de uma estrela até nós, B o seu brilho e L sua luminosidade, esta lei se escreve da seguinte forma [2]:
Para exemplificar, uma lâmpada de 100 Watts pode ter uma luminosidade intrínseca constante, mas pode ser mais brilhante ou não dependendo da distância que se encontra. Uma estrela é “fraca” ou apresenta pouco brilho, por ser pequena, fria, distante ou ambos os três.
Para entender melhor a “Lei do inverso do quadrado” faça o seguinte experimento: tome duas lâmpadas, uma de 100W e outra de 25W. Envolva cada uma numa pequena caixa com uma abertura coberta com uma máscara de papel alumínio e faça um orifício (“pinhole”) por onde a luz emerge.
Em um ambiente escuro, posicione as lâmpadas alinhadas e relativamente próximas uma da outra e observe-as de cerca de 3m de distância. Qual delas parece mais brilhante? Por quê?
Mova a lâmpada que parece menos brilhante e tente encontrar a posição onde ambas parecem ter a mesma luminosidade. A lâmpada de 25W consome quatro vezes menos energia que a de 100W e é quatro vezes menos luminosa. Assim, quando estiver na metade de sua posição original deverá parecer ter o mesmo brilho que a de 100W naquela posição. Você notará que isto não acontece exatamente na posição da metade da distância, como era de se esperar. Aponte as fontes de erros que possam levar a este resultado.
Como exemplo, podemos apontar como uma das fontes de erro a eventual diferença entre as dimensões dos orifícios de cada lâmpada.
A figura abaixo mostra uma maneira simples de entender esta lei [3].
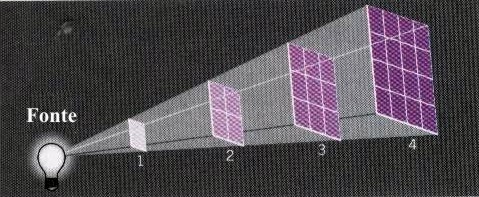
Embora a fonte luminosa emita fótons de luz em todas as direções, consideremos os fótons confinados em linhas retas. Uma vez que fótons viajam geralmente em linhas retas, podemos assumir que nenhum fóton entrará ou sairá da região de confinamento. Certo número de fótons provenientes da fonte luminosa passará por uma área localizada à distância de 1 unidade. À distância de 2 unidades, o mesmo número de fótons passará por uma área que é duas vezes mais larga em cada lado, ou seja, uma área que é quatro vezes mais maior que a localizada na posição 1. Assim, o Brilho Aparente, que é o número de fótons que passam por unidade de área é, (1/2)2 = 1/4. À distância de 3 unidades ele será (1/3)2 = 1/9.
No caso de estrelas, suponhamos que estejamos observando duas estrelas idênticas, porém uma se encontra 5 vezes mais próxima de nós que a outra. A lei do inverso do quadrado nos dirá que a mais próxima parecerá 52, ou seja, 25 vezes mais brilhante que a mais distante. Na recíproca, suponhamos que sabemos, por análise detalhada dos espectros de duas estrelas que elas têm a mesma luminosidade, mas que a observação indica que uma delas é 100 vezes mais brilhante que a outra. Então, podemos deduzir que a aparentemente mais fraca está 10 vezes mais distante, isto porque √100 = 10.
Para testar sua compreensão desta lei procure responder as duas questões abaixo:
- Suponha que ao observar duas estrelas de mesma luminosidade uma delas parece ser 50 vezes mais brilhante que a outra. Se a mais próxima está a uma distância de 12 anos luz. Qual a distância da outra?
- Suponha que uma estrela está a uma distância de 8 anos luz de nós e que uma outra está a 48 anos luz de distância também de nós. As duas estrelas possuem a mesma luminosidade. Quantas vezes mais brilhante a mais próxima parecerá?
A temperatura do Sol pode ser estimada por dois métodos: um que utiliza a Lei de Stefan-Boltzmann e outro que utiliza a Lei de Wien, mas ambos usam propriedades da radiação de corpo negro.
No primeiro método, o fluxo solar integrado em todos os comprimentos de onda FS é a luminosidade por área:
O valor do fluxo solar, fora da atmosfera, medido por detectores em satélites é:
A área é A= 4pR2 e R a distância Terra-Sol, R = 1.5 x 1011 m. Assim, a luminosidade do Sol vale:
A Lei de Stefan-Boltzmann estabelece que sendo o fluxo diretamente proporcional à quarta potência da temperatura, então:
Onde a constante de proporcionalidade s é a chamada constante de Stefan-Boltzmann e vale s = 5.67 x 10-8 J K-4 m-2 s1.
O fluxo solar é também a luminosidade pela área da superfície solar, isto é:
Sendo a área da superfície solar As = 4pRS2 e RS = 7.0 x 10-8 m o raio do Sol. E,
Assim, a temperatura do Sol estimada é:
T = 5,800 K.
O segundo método parte do fato que a temperatura é inversamente proporcional ao comprimento de onda relativo à máxima intensidade de emissão, lP. Esta é base da Lei de Wien que estabelece que:
Onde a constante de proporcionalidade b é chamada constante de deslocamento de Wien e vale b = 2.9 x 10-3 m K
Onde a constante de proporcionalidade b é chamada Constante de Deslocamento de Wien e vale b = 2.9 x 10-3 m K. Assim, a temperatura do Sol é:
T = 5,777 K.
Valor bem próximo do obtido anteriormente.
[1] Adaptado das lições do Telescópio Espacial de Infravermelho Spitzer
[2] Esta dependência se verifica também na interação gravitacional newtoniana e nas interações elétricas.
[3] Adaptado de Discovering Astronomy – Robbins, Jefferys & Shawl – John Wiley & Sons - 1995