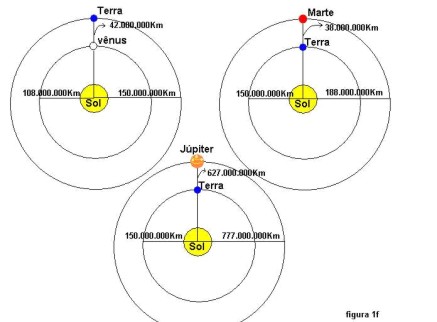
Conforme mostra a figura1f. θ =0,009062rad = 0,52°. De agora em diante sempre que possível utilizaremos a aproximação:
Prof. Renato Las Casas (29/05/2006)
REVISÃO DE ÓPTICA E ALGUNS CONCEITOS
PARTE IIABORDAGEM TEÓRICA DE UM TELESCÓPIO
PARTE IIIA CONSTRUÇÃO
PARTE IVAS CARACTERÍSTICAS DOS TELESCÓPIOS E OBSERVAÇÕES REALIZADAS
PARTE VPROPOSTAS DE UTILIZAÇÃO DOS TELESCÓPIOS
APÊNDICEAS CONTRIBUIÇÕES DE GALILEU GALILEI
CONCLUSÃOAs pessoas podem se interessar por Ciência por vários motivos como curiosidade nata, uma reportagem que viram na televisão, uma experiência que viram ou fizeram na escola ou mesmo acontecimentos intrigantes do cotidiano. A Astronomia talvez seja a ciência que mais atraia a maioria das pessoas, não somente por sua beleza, mas também pelo mistério que representa para todos.
A Astronomia intriga e atrai a humanidade desde quando surgiu o homem. Mesmo nos dias de hoje, da tecnologia e dos avanços no conhecimento do Universo, a Astronomia ainda é muito pouco conhecida pela grande maioria da população. A Astronomia certamente irá continuar a intrigar e atrair a humanidade.
Galileu Galilei aperfeiçoou um instrumento óptico, chamado luneta que servia para ver melhor os astros. Esta novidade marca o início de profundas mudanças no pensamento científico, filosófico e religioso do século XV. Com a luneta de Galileu o modelo Heliocêntrico de Copérnico ganhou enorme credibilidade e o modelo Geocêntrico teve várias de suas teorias completamente descartadas após as observações de Galileu.
Século após século a busca por telescópios melhores e mais potentes prosseguiu, chegou-se ao Newtoniano entre outros. Hoje temos muitos e importantes telescópios que revolucionaram a nossa visão do universo como na época de Galileu. Um telescópio muito especial é o telescópio espacial Hubble que fica fora da atmosfera terrestre. E quando o assunto se trata de imagens de qualidade este telescópio é uma revolução.
Telescópios, devido a sua ampliação nos possibilitam ver detalhes dos corpos celestes que a olho nu não é possível. Isto torna os telescópios, lunetas e binóculos instrumentos extremamente interessantes para as pessoas de um modo geral. Pessoas que nunca olharam um astro através de um telescópio quando o fazem pela primeira vez ficam fascinadas. O interesse pelo funcionamento do instrumento e suas possibilidades de utilização ficam fortemente evidenciados quando se estabelece o contato observador, telescópio e astros. Entre os jovens a curiosidade pelos assuntos da Astronomia está adormecida entre a maioria deles. O contato entre jovem, telescópio e alguns astros como planetas, desperta esta curiosidade e pode levá-los a se interessar bastante por Astronomia e Ciência.
Tendo em vista este poder dos telescópios, decidi construir telescópios relativamente baratos, de fácil construção e o mais eficientes possível. Estes telescópios podem ser construídos por qualquer pessoa e têm um custo bastante inferior aos que podem ser adquiridos em lojas.
Neste trabalho descreverei como construir estes instrumentos, abordarei os aspectos teóricos e farei propostas de utilização. Espero que quem conhecer este trabalho, os telescópios e o que podem observar com eles desmistifiquem estes instrumentos que para a grande maioria dos jovens de famílias de baixa renda parecem tão misteriosos e inacessíveis . Uma das propostas de utilização é seguir o caminho de Galileu Galilei. Então falaremos sobre fases de Vênus, crateras da Lua, seus vales, planícies, montanhas, anéis de Saturno, luas de Júpiter, Via-Láctea entre outros assuntos.
Acreditamos que os resultados esperados para esta experiência serão muito interessantes para estudantes do ensino fundamental, médio e até mesmo para professores formados em Física ou não, que não tiveram a oportunidade de conhecer um pouco melhor Astronomia e sua história ao longo do curso superior. No decorrer do Ensino Fundamental e Médio muitos dos assuntos relativos a telescópios e Astronomia são abordados como história da Ciência que aparece ao longo de todo o percurso escolar, Gravitação Universal de Newton vista no primeiro ano do Ensino Médio e Óptica no segundo ano.
As escolas públicas por terem poucos recursos financeiros assim como os alunos que as freqüentam, levam a uma enorme carência de conhecimento científico e à quase inexistência de experimentos nestas escolas. As propostas que faremos vão ao encontro destas carências devido ao baixo custo de construção dos instrumentos e das várias possibilidades de utilização. A presença de um telescópio de boa qualidade nestas escolas irá despertar a curiosidade entre os estudantes e com esta curiosidade despertada o resultado das experiências terão resultados muito positivos. Quando eu concluir o curso de Física Licenciatura e estiver trabalhando na rede pública ou mesmo particular, pretendo colocar em prática e divulgar o trabalho exposto aqui.
Nesta parte revisarei alguns conceitos de óptica e também comentando algumas propriedades do olho humano. Esta revisão tornará mais fácil o entendimento do que será exposto adiante.
As lentes são instrumentos ópticos que tem por objetivo desviar de maneira regular os raios de luz. Este desvio regular é o que nos permitirá utilizá-las. Dizer que um instrumento desvia de maneira regular os raios de luz, significa que é possível prever a trajetória de qualquer raio incidente no instrumento.
Uma das características de uma lente convergente é que todo raio que chega paralelamente ao seu eixo ótico sai da lente passando pelo seu foco. A figura 1a mostra esta característica.
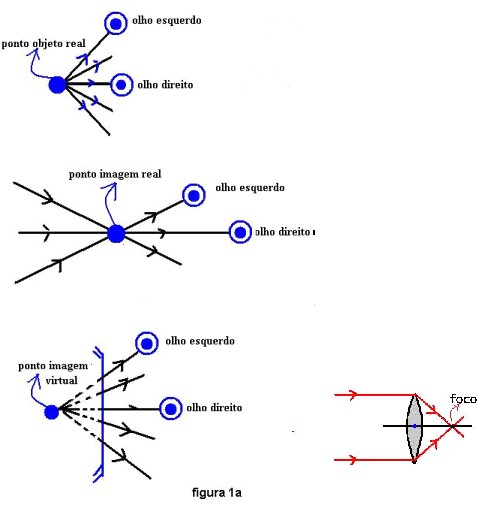
A figura mostra um ponto objeto real, os raios que saem deste objeto divergem e o local de onde saem os raios existe de fato um objeto. Também um ponto imagem real, os raios que saem da imagem divergem, mas no local onde está esta imagem não há objeto algum, mas somente luz, e uma imagem virtual, o local onde está esta imagem não possui nem objeto nem luz.
O cérebro foi programado para produzir a imagem onde ocorre o cruzamento dos raios que atingem o olho esquerdo e direito. O triângulo formado pelos olhos e o objeto é o que determina a localização da imagem. A imagem é produzida pelo cérebro onde se cruzam os raios no caso de objetos reais e imagens reais e onde se cruzariam os raios no caso de imagens virtuais.
A eq/1a é chamada equação de Gauss para lentes e espelhos e é válida considerando algumas aproximações. Para raios incidentes praticamente paralelos esta equação dá excelentes resultados. A grandeza f é chamada distância focal e para lentes convergentes tem um valor positivo, di é a distância da imagem à lente e será positiva para imagens reais e negativa para imagens virtuais, “do” é a distância do objeto à lente e será sempre positivo.
Chama-se de altura do objeto ou da imagem o seu tamanho transversal em ralação ao eixo óptico da lente. A altura do objeto será chamada aqui de Ho e a altura da imagem será chamada de Hi. Estão relacionados pela seguinte equação:
Lentes podem ser associadas e juntas formam uma nova lente. Este conjunto de lentes associadas pode ser tratado como se fosse uma única lente. Se a distância entre cada uma delas e as outras é praticamente nula podemos utilizar a seguinte equação para associação de lentes:
Onde F é a distância focal da nova lente, resultante da associação, f1, f2...fn são as distâncias focais individuais de cada lente da associação.
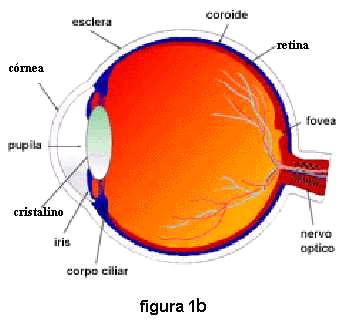
O olho humano é um complexo sistema óptico que tem a função de interagir com a luz ambiente e enviar estímulos elétricos ao cérebro. O envio de estímulos elétricos ao cérebro é possível graças a reações químicas.
O cristalino é uma lente convergente de distância focal ajustável e a retina é uma superfície composta de células sensíveis à luz visível. O cristalino associado com a córnea forma uma lente convergente que projeta uma imagem real e invertida na retina, assim cada célula é estimulada de maneira diferente, estes diferentes estímulos levados ao cérebro permitem a ele produzir a imagem.
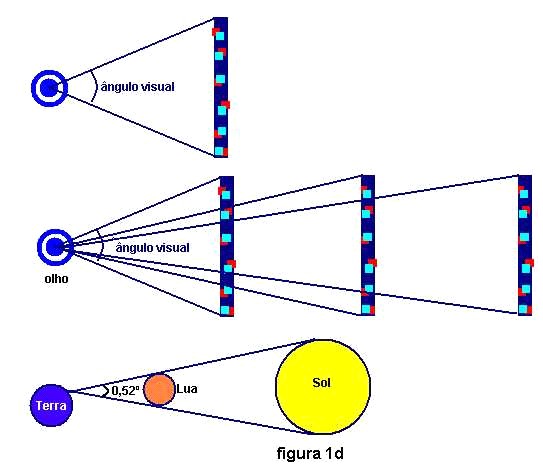
A figura 1d mostra que quanto mais distante um objeto está, menor é o ângulo visual. O tamanho que um objeto parece ter para nós depende deste ângulo visual e não apenas do tamanho do objeto. Por isso que um astro tão pequeno como a Lua parece ser do mesmo tamanho de um astro tão imensamente maior como o sol. A figura 1d mostra que o ângulo visual para o Sol e a Lua é de aproximadamente 0,52º. Aqui trabalharei bastante com o ângulo visual.
Fazer com que objetos distantes pareçam maiores é o objetivo do instrumento óptico deste trabalho, que é o telescópio.
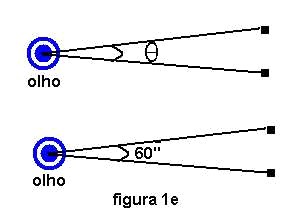
A figura 1e mostra dois pontos e um olho a observar estes pontos segundo um certo ângulo visual, se os olhos forem se afastando o ângulo visual diminui e os pontos parecem se aproximar. Chegará um momento em que o observador não mais distinguirá se está vendo um ou dois pontos, se são três, se os pontos estão alinhados na horizontal ou na vertical, etc. O ângulo mínimo que permite a distinção de dois pontos é chamada de resolução do olho humano. Se um objeto está tão distante que não podemos dizer qual é a sua forma, dizemos que seu ângulo visual é menor que a resolução do olho humano, se no entanto formos capazes de dizer qual é a forma do objeto que vemos podemos dizer que o ângulo visual do objeto é maior ou igual à resolução do olho humano. Claro que existem objetos mais fáceis e mais difíceis de serem resolvidos, não é apenas uma questão de olho, mas também uma questão de interpretação do cérebro.
A resolução varia de pessoa para pessoa, mas considera-se normal uma resolução de 60” (sessenta segundos de arco). Objetos com ângulos visuais menores que 60” não nos permite a olho nu descrever sua forma, não podemos dizer se é um círculo, quadrado, se são um ou dois objetos, etc. Por isso a olho nu não podemos ver as crateras da Lua, os anéis de Saturno, as fases de Vênus ou certos detalhes da cabeça de uma formiga. Claro que existem pessoas com olhos que apresentam resoluções maiores e menores do que 60”.
Mesmo se a retina tivesse infinitas células, a resolução não poderia ser melhor que 20" de arco devido à limitação da difração sofrida pela luz ao atravessar a pupila. A melhor resolução que um instrumento óptico com abertura circular de diâmetro d pode obter é dada pelo critério de Rayleigh. O ângulo em radianos é dado por:
Supondo que o comprimento de onda seja 589nm e que o diâmetro da pupila seja varie de 2mm a 9mm e utilizando critério de Rayleigh, chegamos aos seguintes ângulos mínimos: 74,1” para d=2mm e 16,46" para d=9mm.
A limitação da resolução de um instrumento óptico pelos efeitos da difração é uma imposição inevitável da natureza. O critério de Rayleigh nos dá a melhor resolução que um instrumento pode apresentar, não sendo possível obter resoluções melhores do que as permitidas por este critério.
1
Qual é o ângulo visual de:
a)A Lua?
b)Vênus, quando o mais próximo possível da Terra?
c)Marte, quando o mais próximo possível?
d)Júpiter quando o mais próximo possível?
Resposta:
a) A distância Terra-Lua é de aproximadamente 384.000Km e visto que o ângulo visual é pequeno podemos dizer que: θ =3.480Km/384000Km.
Conforme mostra a figura1f. θ =0,009062rad = 0,52°. De agora em diante sempre que possível utilizaremos a aproximação:
b)Conforme mostra a figura1f a menor distância entre a Terra e Vênus é de 42.000.000Km, o ângulo visual é então θ =12.100Km/42.000.000Km=0,000288rad= 0,0165º=59,4” que é menor que a resolução do olho humano e assim não podemos ver suas fases. Claro que quando Vênus estiver o mais próximo possível da Terra não é possível vê-lo, pois visualmente está muito próximo do Sol.
c)Conforme mostra a figura a menor distância entre a Terra e Marte é de aproximadamente 38.000.000Km, então θ =6750Km/38.000.000Km=0,000177rad =0,0101º=36,6”.
d)Conforme a figura 1f podemos ver que o ângulo visual de Júpiter nestas condições é de θ =143.000Km/627.000.000Km=0,000228rad=0,013º=47,04”
Exemplo 2
A que distância da lente aparece um objeto localizado a uma distância muito grande desta lente?
Resposta:
Vamos responder primeiro utilizando a eq/1a:
Esta resposta mostra que quando um objeto está muito distante de nós como a Lua a imagem desta, quando utilizamos uma lente convergente para observá-la, aparece no foco da lente. Esta mesma conclusão pode ser tirada lembrando que os raios de luz provenientes de corpos distantes chegam praticamente paralelos aqui. Olhando a figura 1a podemos chegar à mesma conclusão
percebendo que raios que chegam paralelamente ao eixo principal da lente a atravessam e se cruzam no foco.O objetivo de um telescópio é fazer parecer muito maior do que vemos a olho nu um objeto distante como um astro por exemplo. Ver um objeto maior pode ser conseguido das seguintes maneiras: aumentando o objeto de tamanho, nos aproximando do objeto, o objeto se aproximando de nós ou utilizando um instrumento óptico. Em astronomia é mais fácil a última maneira já que ir até o astro não é fácil, esperar uma aproximação apreciável é impossível para a maioria dos corpos, nos resta então utilizar um instrumento óptico capaz de ampliar a imagem que conseguimos a olho nu.
Telescópio refrator é composto basicamente de duas lentes. A chamada objetiva é a lente que coleta a luz vinda do objeto e produz uma imagem real e invertida deste objeto no seu foco conforme já vimos no exemplo 2 da parte I, se estivermos lidando com um astro. A outra lente é chamada de ocular e é nesta lente que é obtida a imagem final do objeto quando olhamos através dela. Seu objetivo é ampliar a imagem real gerada pela objetiva. O restante dos equipamentos de que é feito o telescópio servem para facilitar as observações e impedir que luz indesejável, ou seja, evitar que luz não proveniente do astro chegue até o olho do observador. A base móvel facilita localizar e manter o telescópio apontado para o astro. O tubo enegrecido por dentro serve para segurar as lentes e impedir a entrada de luz indesejável.
Normalmente a lente objetiva tem distância focal grande em relação à distância focal da lente ocular. Quando a objetiva gera uma imagem real de um astro no seu foco é como se ela colocasse no seu foco uma miniatura do astro que pode ser vista ampliada pela ocular. A lente ocular de um telescópio funciona como uma lupa sendo utilizada para examinar um pequeno objeto ao alcance das mãos.
Aberração esférica é um indesejável efeito que ocorre quando o foco da lente não é o mesmo para qualquer raio, ou seja, onde é o foco depende de por onde entrou o raio, mesmo o feixe sendo de raios paralelos. Este efeito gera distorções na imagem e pode ser minimizado fazendo a lente ter curvas apropriadas, ou seja, ter curvas que façam com que qualquer que seja o ponto de incidência de raios paralelos, estes após atravessarem a lente, convirjam para o mesmo ponto: o foco único.
Aberração cromática é um indesejável efeito que ocorre quando luz policromática ao passar por um meio transparente (como uma lente) em certos ângulos é decomposta nas suas várias cores, sendo que o problema reside no fato de que cada cor se desvia num ângulo diferente, resultando numa imagem com contornos coloridos indesejáveis.
Primeiro examinemos como uma lente convergente faz parecer maior do que é um pequeno objeto ao ser examinado pela mesma.
Visto que o cristalino é uma lente de distância focal ajustável, podemos ver objetos tão distantes como a Lua ou tão próximos como a página de um livro quando fazemos uma leitura. No entanto existe uma distância mínima que um objeto deve estar para que possamos vê-lo nitidamente. Esta distância mínima varia de pessoa para pessoa e com a idade. Míopes têm esta distância pequena, hipermétropes têm esta distância maior. Admitirei como um valor normal esta distância sendo de 20cm.
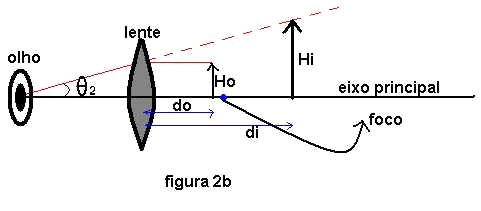
Ao falar da ampliação angular de uma lente, estarei comparando com esta distância. Quando disser que uma lente está aumentando a imagem de um objeto em 10 vezes, quero dizer que se olhássemos o objeto a 20cm e depois o olhássemos com a lente, a imagem pareceria 10 vezes maior do que quando observamos o objeto a 20cm.
A figura 2a mostra um observador olhando um objeto à distância mínima que lhe permite ver com nitidez. A figura 2b mostra o observador olhando para o mesmo objeto através de uma lente convergente de pequena distância focal, digamos uns 10cm.
As figuras 2a e 2b não estão em escala, normalmente os raios mostrados são mais paralelos ao eixo principal e os ângulos q1 e q2 são bastante pequenos.

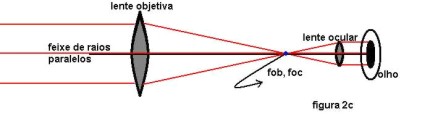
A figura 2c mostra em esquema um telescópio refrator, é possível ver a lente objetiva, a ocular, os focos e os raios. Este telescópio é chamado de refrator porque se utiliza da lei da refração para gerar as imagens. A lente objetiva desvia de maneira regular os raios que nela chegam. Este desvio é conseguido graças ao fato de esta lente ser feita de um material com um certo índice de refração. É o desvio regular da luz feita pela objetiva que permite a utilização do telescópio. Se ao invés da lente objetiva tivéssemos um espelho curvo teríamos um telescópio refletor.
O olho realiza o menor esforço quando olhamos para objetos distantes, olhar para objetos próximos faz com que os músculos que controlam o cristalino fiquem tencionados. Quando olhamos para um objeto muito distante dizemos que estamos com as vistas desarmadas, ou seja, os músculos que controlam o cristalino ficam relaxados. Na situação da figura 2c os raios chegam paralelos ao olho o que significa comodidade para observação, a situação mais confortável ocorre quando os focos das lentes coincidem. Se os focos não coincidem, os raios não chegam paralelos ao olho e o cristalino tenta se acomodar para obtermos uma imagem nítida, conforme o caso o cristalino consegue, mas as vistas se tornam cansadas, às vezes o cristalino atinge seu limite de ajuste e não se pode obter uma imagem nítida, daí a razão de a posição da ocular ser ajustável nos telescópios, cada pessoa individualmente deve procurar a melhor distância entre a ocular e a objetiva de modo a obter uma imagem nítida e sem esforço visual.
Queremos saber quantas vezes maior fica a imagem do objeto vista pelo telescópio em relação à imagem quando o objeto visto a olho nu.
Vamos analisar o tamanho da imagem formada pela objetiva:

A lente ocular tem por objetivo ampliar, ou seja, examinar de perto como se fosse uma miniatura a imagem gerada pela lente objetiva. Conforme já mostrei seu aumento é dado por:
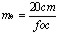
O ângulo visual da imagem real pode ser dado pela razão entre sua altura e 20cm, quando vista o mais próximo possível. Chamarei este ângulo de Â1. Então Â1=altura da imagem real/20cm.
Quando vista pela ocular esta imagem será aumentada de m, ou seja, será aumentada de 20cm/foc.
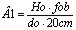
Então o novo ângulo da imagem quando vista pela ocular será:
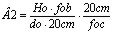
Queremos agora saber a razão entre o ângulo visual  do objeto quando visto a olho nu e o ângulo Â2 quando visto pelo telescópio, ou seja, queremos saber quantas vezes aumenta o telescópio com estas lentes.

A eq/2b nos dá o número de vezes que o telescópio aumenta o tamanho da imagem do objeto em relação à imagem quando o objeto visto a olho nu. A imagem final vista através da lente ocular é virtual e invertida o que não é um problema para observações astronômicas já que o céu não tem um lado de baixo ou de cima. A eq/2b funciona se os planos focais da objetiva e da ocular forem muito próximos ou coincidentes o que acontece na prática devido à relativa dificuldade do cristalino de mudar muito sua distância focal.
Olhando apenas para a eq/2b parece que obter grandes aumentos é muito fácil bastando para isto diminuir bastante foc e aumentar fob o que não é muito difícil. Mas as coisas não são tão simples assim porque a ampliação de um telescópio é apenas uma de suas características. Podemos sim aumentar o quanto pudermos, mas grandes aumentos poderão resultar em perda da qualidade da imagem. Precisamos pensar na quantidade de energia luminosa que chega na retina quando vemos uma imagem através de um telescópio. Grandes aumentos levam a uma diminuição do fluxo de energia luminosa sobre a retina resultando em má qualidade da imagem.
A resolução de um telescópio é a sua capacidade de gerar imagens com mais detalhe possível. Uma grande resolução significa que podemos ver detalhes do objeto, podemos por exemplo ver pequenas crateras em grandes crateras da Lua onde a olho nu nem sequer as grandes crateras podem ser vistas. A resolução de um telescópio é representada pelo menor ângulo visual no qual é possível resolver ou distinguir dois pontos. Portanto a resolução pode ser dada em segundos de arco. A resolução do telescópio neste trabalho será estudada considerando que apenas o olho humano será utilizado nas observações. Se ao invés do olho humano se utilizasse um equipamento como um sensor de câmera fotográfica digital, a resolução do telescópio daria resultados diferentes. Aqui a resolução do telescópio é apenas a resposta à pergunta: Qual é o ângulo visual que multiplicado pela ampliação M do telescópio resulta em 60"? Lembrando que 60" é considerada a resolução do olho humano.
A retina é uma superfície composta de células sensíveis à luz e cujos agentes principais são os foto receptores. Os foto receptores são os cones, que são os responsáveis pela sensação de cor, e os bastonetes que são responsáveis pela sensação da intensidade luminosa, sendo que os bastonetes não participam da sensação de cor. Os cones além de participarem na sensação de cor também contribuem para a sensação de intensidade luminosa.
Na região da retina responsável pela visão existe em todas as partes cones e bastonetes, no entanto na região central da visão existe o predomínio dos cones e na região periférica o número de bastonetes supera em muito o de cones.
Os bastonetes são muito mais sensíveis à luz do que os cones que somente respondem a estímulos luminosos se a intensidade for forte. Por esta razão quando estamos em um ambiente escuro vemos tudo em preto e branco ou com muita pobreza de cores. Geralmente quando temos pouca luz a percepção de cor fica bastante prejudicada.
O funcionamento dos cones e bastonetes se dá através de reações químicas devido à absorção de energia luminosa, em que há a combinação e recombinação de ligações em uma proteína chamada rodopsina, presente nas células da retina. Se a intensidade da luz é normal a reposição desta proteína não é afetada e enxergamos normalmente. Se no entanto a intensidade luminosa for muito intensa, não há tempo para repor a rodopsina transformada na reação química. O resultado é que as células não respondem mais adequadamente aos estímulos, ficam incapazes de distinguir a diferença de intensidade e as vistas ficam ofuscadas pelo brilho.
O contraste é uma característica da imagem relacionada com a riqueza de tonalidades de cor e brilho. Um bom contraste significa que podemos perceber pequenas diferenças de tonalidades de azul por exemplo. Um bom contraste significa também que podemos perceber com clareza as partes claras e escuras da imagem, ou seja, podemos perceber a riqueza de brilhos da imagem. O que é escuro fica muito escuro em relação ao que é claro (brilhante). Um mau contraste por outro lado significa que as cores parecem ser todas da mesma tonalidade, a imagem fica meio cinzenta, com pobreza de cores. Partes claras e escuras parecem ter o mesmo brilho. O contraste influencia na resolução e posteriormente mostrarei uma condição que garante que a imagem terá sua qualidade otimizada.
A nitidez é a impressão final que temos da imagem e está relacionada com a resolução, contraste e o olho de quem observa. A nitidez pode ser prejudicada tanto quando temos muita luz chegando na retina, assim como quando temos pouca luz. Se olhamos por exemplo para um farol aceso de um carro, não podemos ver detalhes da lâmpada ou do espelho, porque as células da retina ficam fora do seu limite de funcionamento devido à grande quantidade de luz, a imagem fica pobre de detalhes e de cores. Quando olhamos por exemplo Júpiter com um telescópio que está aumentando excessivamente não podemos ver os detalhes da sua superfície e este planeta parece ter uma mesma cor branco amarelada, este por exemplo é um caso de pouca luz prejudicando a nitidez da imagem.
Agora procuraremos uma condição para que os aumentos proporcionados pelo telescópio não prejudiquem a qualidade da imagem.
Fluxo é a razão entre a potência irradiada por uma fonte e a área pela qual esta radiação está distribuída para uma certo ponto distante da fonte. É dada por:
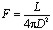
Onde L é a chamada luminosidade intrínseca e é a potência irradiada pelo corpo e dada em watts. D é a distância à fonte que é o raio da possível esfera cujo centro é o corpo que irradia, lógico que a esfera deve interceptar o ponto no qual estamos definindo o fluxo. O fluxo do Sol, por exemplo, à distância que estamos dele é de aproximadamente 1440 watts por metro quadrado. .
O cristalino em conjunto com a córnea formam uma lente que projeta uma imagem real e invertida na retina. Esta imagem ocupa uma área “ao". O telescópio por causa do seu aumento, aumenta a área desta imagem na retina. Pensando em fluxo vemos que ele pode aumentar ou diminuir conforme o telescópio, ou seja, se o telescópio aumenta muito, o fluxo pode ficar baixo e a imagem ficar fraca, ruim com baixo contraste. Este é um sério problema em telescópios e que será analisado.
Queremos que o telescópio aumente, mas sem perder a qualidade da imagem. Pensemos primeiro no seguinte: Será que o fato de a área da lente objetiva ser maior do que a área da pupila é um fato suficiente para compensar o aumento da imagem?
Quando um telescópio amplia, em relação a olho nu, a imagem de um objeto é como se o observador fosse levado para um ponto entre o telescópio e o observador. Ser levado aqui significa que a imagem vista pelo observador através do telescópio teria o mesmo tamanho que quando vista a olho nu pelo observador neste ponto. Para ficar mais claro pensemos no seguinte: Se estamos perto de uma montanha, o ângulo visual desta montanha é Â, quando nos afastamos da montanha o ângulo visual diminui. Mas através do telescópio, podemos aumentar o ângulo pequeno quando observamos de longe de tal maneira que obtemos o ângulo visual  novamente. Então é como se o telescópio nos levasse novamente para perto da montanha. Daqui para frente estarei me referindo a este fato dizendo que o telescópio leva as vistas para uma certa distância do objeto. Lembrando que a imagem vista pelo telescópio não é a mesma que veríamos se fossemos onde ele levaria nossas vistas, a imagem tem apenas o mesmo tamanho. Procurarei aqui uma condição para que a imagem vista pelo telescópio tenha pelo menos o mesmo fluxo na retina se estivéssemos de fato onde ele leva as vistas.
Vejamos qual é a relação entre o número de aumentos proporcionados pelo telescópio e a distância que ele nos leva ao objeto.
Vamos chamar de Â1 o ângulo visual quando o observador observa um objeto de altura Ho e de D a sua distância a este objeto. Se o objeto está distante, Â1 é pequeno e pode ser dado por:
Â1=Ho/D
Vamos agora imaginar que estamos onde o telescópio leva nossas vistas. O novo ângulo visual será Â2 que também poderá ser dado por:
Â2=Ho/d, onde d é a distância ao objeto para qual o telescópio levou nossas vistas na observação.
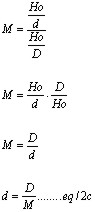
A eq/2c nos mostra que o telescópio divide a distância visual entre o observador e o objeto pelo número de aumentos que ele proporciona. Quando observamos o Sol com um telescópio que aumenta apenas dez vezes é como se estivéssemos mais próximos do Sol do que Mercúrio, pois 150.000.000Km/10=15.000.000Km. Mercúrio está a 57.000.000Km do Sol.
O aumento que o telescópio proporciona diminui o fluxo na retina. A área da lente objetiva ser maior que a da pupila contribui para o aumento do fluxo na retina. Vamos agora procurar uma condição onde há equilíbrio entre as duas características opostas citadas anteriormente. Queremos que a imagem vista pelo telescópio seja a mesma que quando vista onde ele nos leva, ou seja, queremos que o fluxo na retina seja o mesmo quando vemos uma imagem pelo telescópio ou quando vamos pessoalmente onde ele nos leva e olhamos a olho nu o objeto neste lugar.
Vamos supor que toda a energia coletada pela objetiva chegue na retina o que é aproximadamente verdadeiro. Antes de prosseguir vamos nomear algumas variáveis.
| Variável | O que ela representa |
|---|---|
| Fl | Fluxo que chega na lente objetiva |
| Fp | Fluxo que chega na pupila quando o observador está onde o telescópio o levaria. |
| Pl | Potência que chega na área Al da lente objetiva |
| Al | Área da lente objetiva |
| Fr | Fluxo na área “ao” da imagem sobre a retina |
| Lf | Luminosidade da fonte |
| ao | Área da imagem na retina |
| a | Área da pupila |
| Dl | Diâmetro da objetiva |
| Dp | Diâmetro da pupila |
| d | Distância para a qual o telescópio leva nossas vistas |
| D | Distância do observador ao objeto |
| Pp | Potência que chega na pupila se o observador fosse de fato onde |
Vamos procurar o fluxo na área “ao” utilizando o recurso do telescópio:
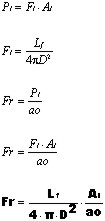
Esta última equação nos mostra que o fluxo na retina é proporcional ao brilho da fonte, à área da objetiva e inversamente proporcional à distância do objeto e à área ocupada pela imagem na retina.
Vejamos agora qual seria o fluxo na área “ao” da imagem na retina se fossemos onde o telescópio nos leva:
Primeiramente observemos que “ao” é o mesmo nas duas situações, pois é exatamente esta a condição que procuramos, ou seja, queremos que a imagem tenha o mesmo tamanho dado por “ao” e o mesmo brilho que dependerá do fluxo na área “ao”.
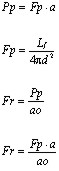
Esta última equação nos mostra que o fluxo na área “ao” da imagem na retina é proporcional ao brilho da fonte, à área da pupila e inversamente proporcional a “ao” e a d.
Utilizando a eq/2c obtemos:
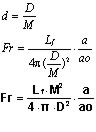
Claro que queremos que Fr=Fr, ou seja, queremos que o fluxo na área “ao” da retina seja o mesmo nas duas situações.
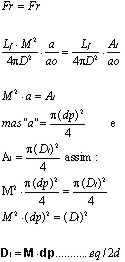
A eq/2d é a condição para que o fluxo na área “ao” da imagem na retina seja o mesmo que o fluxo se estivéssemos onde o telescópio leva as vistas. Chamarei este M de agora em diante de Mr, que é a abreviatura de M referência. Não chamarei de M ideal, porque haverá casos em que se desejará aumentar mais do que Mr recomenda e haverá casos em que se desejará aumentar menos do que Mr recomenda. Mas com certeza Mr representa o aumento que garante que o fluxo na retina é o mesmo nas duas situações: vendo o corpo pelo telescópio ou sem o telescópio e indo pessoalmente onde ele levaria os nossos olhos.
A relação Dl=(Mr)dp nos mostra que não podemos aumentar arbitrariamente o tamanho da imagem de um objeto sem mudar o fluxo na retina. Mostra também que quanto maior o diâmetro da objetiva, mais se pode aumentar sem perder a qualidade da imagem. Esta relação é válida também para telescópios refletores bastando substituir Dl por “De” que é o diâmetro do espelho, por isso é que se busca telescópios com espelhos de grandes diâmetros.
A relação Dl=(Mr)dp pode ser escrita também como: Mr=Dl/dp e nos mostra o Mr é proporcional ao diâmetro da lente e inversamente proporcional ao diâmetro da pupila. Mr ser proporcional a Dl é óbvio, mas parece contraditório ser inversamente proporcional a dp. A contradição desaparece quando lembramos que ao procurar a relação Dl=(Mr)dp fizemos uma comparação entre fluxo a olho nu e fluxo com o telescópio. A aparente contradição desaparece quando lembramos que se a pupila está dilatada é porque temos pouca luz, e se temos pouca luz não podemos aumentar demais a imagem devido ao baixo fluxo.
Na prática não se utiliza os telescópios aumentando somente segundo a eq/2d , porque ela exige grandes diâmetros para as lentes objetivas ou espelhos. Costuma-se aumentar muito mais do que a eq/2d receita, claro que a imagem vista perde um pouco da qualidade, mas conforme M se afasta do M referência a imagem não fica tão ruim assim e em se tratando de astros como a Lua é até desejável aumentar muito, pois este astro é muito brilhante. No caso de galáxias por exemplo já se deseja M até menor que o referência, pois o brilho é muito pequeno. A eq/2d serve para pelo menos nos dar uma noção de o quanto estamos nos afastando da suposição de que a imagem vista através do telescópio é a mesma se fossemos onde este leva nossas vistas.
Quando um telescópio aumenta mais e mais, podemos ver mais detalhes do objeto. Quanto mais aumentamos, mais detalhes vemos. Vimos que quanto mais detalhes de uma imagem podemos ver melhor é a resolução. No entanto chegará um momento em que não mais adiantará aumentar a imagem afim de obter melhor resolução. O telescópio tem um limite para M que permite melhores resoluções, ou seja, depois de atingido um certo M não adianta mais aumentar a imagem afim de se ver mais detalhes. Podemos entender isto lembrando do que foi dito a respeito de resolução, contraste, nitidez e aumentos.
Chamarei de resolução simples a resolução que podemos obter com o telescópio, levando em conta apenas o seu aumento, a distância do objeto e a resolução do olho humano. Claro que a resolução de um telescópio depende de vários fatores como: turbulência da atmosfera, diâmetro da lente objetiva, olho do observador, absorção pelos componentes do telescópio, condições de iluminação do corpo observado, entre outros fatores. A resolução simples no entanto pode estar próxima da realidade dependendo da relação Dl=(Mr)dp. Quanto mais próximo do M referência mais próximo da realidade estará a resolução simples. Vejamos como encontrá-la:
A resolução simples é o ângulo que multiplicado pelo aumento do telescópio resulta num ângulo igual à resolução do olho humano. A resolução simples nos dá portanto o menor ângulo visual de uma parte de um objeto que pode ser resolvida utilizando o telescópio. A resolução simples é a resolução máxima que um telescópio poderia chegar. As resoluções reais são sempre piores que a resolução simples. Então 60”=Rs(M).
Rs=60”/M........eq/2e
Por se tratar de um ângulo visual a respeito de parte do objeto, a resolução simples pode ser usada para calcular o menor tamanho transversal que parte de um objeto deve ter para que possamos resolvê-la. A resolução simples determina o tamanho mínimo de um objeto que nos permite identificá-lo, ou seja, dizermos qual é a sua forma. Chamaremos de Tmin este comprimento mínimo.
Tmin = (Rs)(D) ......eq/2f
Onde D é a distância do observador ao objeto e Rs é a resolução simples em radianos. Visto que Tmin está sujeito a Rs sua determinação fica limitada também às condições de determinação da Rs. Lembrando que a resolução do telescópio será o ângulo visual mínimo a olho nu que ao ser aumentado pelo telescópio se torna igual a 60” de arco.
Exemplo 1
Qual é o ângulo visual de Júpiter quando este está o mais próximo possível da Terra e é observado através de um telescópio de fob=2000mm, e foc=50mm?
Resposta:
Conforme o exemplo 1 do capítulo 1 o ângulo visual de Júpiter quando visto a olho nu é de 0,013º. M=2.000mm/50mm=40. Então o ângulo visual do planeta ficará 40 vezes maior, fazendo o produto obtemos: 0,52º que é o ângulo visual da Lua.
Exemplo 2
Qual é o Mr segundo a eq/2d do telescópio do exemplo anterior supondo que o diâmetro da lente seja de 30mm e diâmetro da pupila seja de 5mm?
Resposta:
Mr=Dl/dp
Mr=30mm/5mm
Mr=6
Notemos que este valor é muitas vezes menor do que as quarenta vezes obtidas com este telescópio. A conseqüência para este fato é que a imagem de Júpiter não será a mesma se o víssemos quarenta vezes mais próximo. Não será possível ver detalhes da sua superfície, pois 40 vezes está muito distante de 6 vezes. Temos um bom ângulo visual, mas não temos um bom contraste nestas condições.
Exemplo 3
Qual é o tamanho mínimo de um objeto na Lua que pode ser resolvido utilizando um telescópio de fob=2000mm e foc=6mm?
Resposta:
Segundo a eq/2f temos
Tmin=(Rs)(D)

Claro que este valor é maior do que a realidade. Tmin é algumas vezes maior do que isto por causa de fatores já citados anteriormente como: diâmetro da objetiva, interferência da atmosfera e limitações da visão.
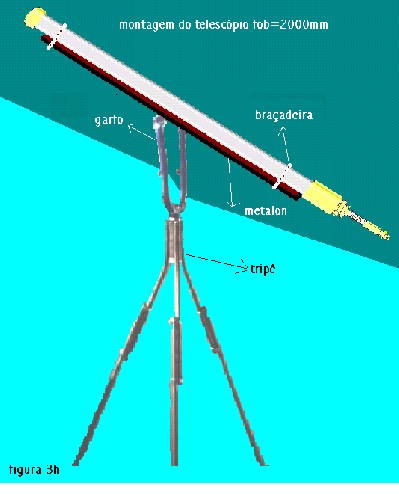
Os telescópios foram construídos de modo a serem o mais barato e eficientes possível. São compostos de três partes: o telescópio de 920mm, um tubo com uma lente de 2000mm e a base móvel que serve para facilitar as observações sendo que é possível utilizar o telescópio de 920mm sem a necessidade desta base. O telescópio 2000mm depende fortemente da base móvel devido a seu maior aumento e também por causa do seu tamanho.
A base móvel que foi construída tem as seguintes características: possibilita apontar para qualquer ponto do céu, apresenta movimentos suaves e estáveis, é desmontável, de fácil transporte, é leve, teve um baixo custo e sua construção foi relativamente fácil.
Para sua construção primeiramente foi feito um planejamento visando facilitar a aquisição dos materiais, evitar desperdícios e encarecimento dos serviços prestados por terceiros.
| Quantidade | Equipamento, material ou serviço | Preço total Mínimo(R$) | Onde encontrar |
|---|---|---|---|
| 6 | Braçadeiras 22-32 | 4,90 | Casa de ferragens |
| 1 | Cano de aço de 35mm de diâmetro e comprimento 120mm | 1,00 | Igual ao anterior |
| 1,5 metros | Metalon 40mm por 30mm | 8,00 | Igual ao anterior |
| 4,5 metros | Tubo de aço 3/8, diâmetro 15mm | 8,40 | Igual ao anterior |
| 1 | Kit garfo de bicicleta pequena | 18,00 | Oficina de bicicletas ou lojas de equipamentos de bicicletas |
| 2 | Bacia da direção de bicicleta com diâmetro maior de aproximadamente 38mm | 1,40 | Igual ao anterior |
| 1 | Cubo de roda dianteira da roda de bicicleta grande | 3,00 | Igual ao anterior |
| 1 | Eixo do cubo acompanhado de suas duas porcas | 1,00 | Igual ao anterior |
| 2 | Arruela 1 polegada | 0,60 | Igual ao anterior |
| 1 | Tira de retalho | 0,50 | Costureira |
| ----- | Serralheria | 10,00 | ---------- |
| Total | 56,80 |
A tabela acima mostra em resumo os equipamentos e materiais utilizados na construção da base móvel. Falaremos sobre cada item visando uma aquisição eficiente e mais barato.
As braçadeiras são anéis de aço com um parafuso que permite ajustar seu diâmetro. Visto que são de aço podem abraçar, ou seja, apertar com firmeza equipamentos que possam passar por dentro de sua circunferência. Aqui elas servem para prender um par de tubos de aço 3/8 garantindo assim a fácil montagem e desmontagem da base.
O cano de aço de 35mm de diâmetro por 12cm de comprimento pode ser adquirido tanto na serralheria como na casa de ferragens como sobra. Este cano servirá para prender o garfo e também para receber através de soldagem os tubos 3/8 que serão as pilastras da base.
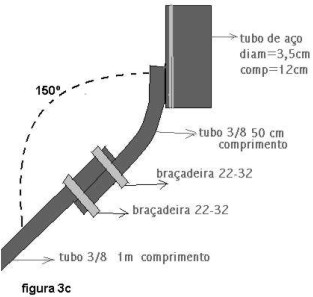
Quando comprei os tubos 3/8 pedi para que serrassem os 4,5 metros em 6 partes: três partes de 1m de comprimento cada e três partes de meio metro cada. Isto não acarretará em aumento de preço. A figura 3c mostra a soldagem de um dos tubos 3/8 e as braçadeiras.
O kit garfo é um conjunto de peças de bicicletas composto de um garfo de bicicleta de preferência pequeno e que tenha inclinação. Composto também pelas porcas, arruelas e esferas que possibilitam prendê-lo ao cano de aço de 12cm de comprimento. O que é importante é que o garfo seja barato, tenha uma pequena inclinação e tenha seus acessórios: as porcas, aranhas com as esferas e arruelas.
As bacias de direção são pequenos componentes que servirão para se acoplar ao cubo e garantir o atrito estático no movimento do metalon. O diâmetro maior de aproximadamente 38mm é essencial para o encaixe com o cubo.
O cubo é um equipamento da roda que serve para prender os raios, onde o cubo recebe o eixo da roda. O cubo utilizado é o da roda dianteira por ser menor, mais simples e mais barato.
O cubo foi soldado no centro do metalon. Para prendê-lo ao garfo a conexão foi feita através do cubo e do eixo com duas arruelas, duas porcas e as duas bacias de direção. A figura 3a mostra em esquema as peças antes de serem apertadas as porcas e o conjunto se tornar firme.
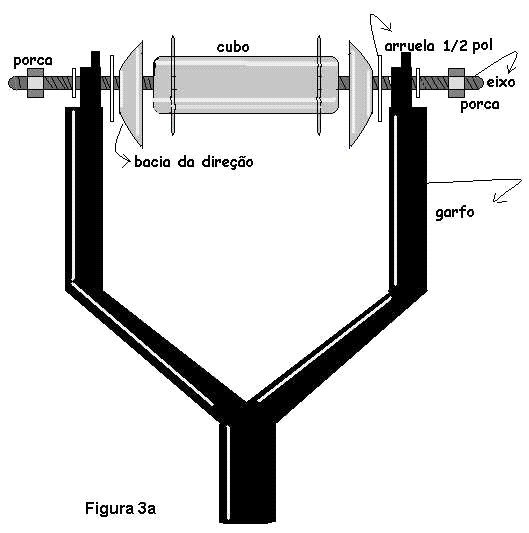
A montagem da base foi relativamente simples, primeiramente adquiri os materiais conforme já descrito, depois anotei em uma folha instruções para levar ao serralheiro. As instruções serão descritas a seguir.
Levei o metalon, o cubo, os três tubos 3/8 de meio metro cada, o cano de aço de 12cm de comprimento que foi preso ao garfo. Pedi ao serralheiro que soldasse o cubo no centro do metalon.
Os tubos 3/8 foram soldados simetricamente ao cano de aço, mas antes foram encurvados de aproximadamente 30º, ou seja, o segmento do tubo soldado ao cano de 12cm de comprimento deverá formar um ângulo de aproximadamente 150º com o segmento que teve a direção modificada. O serralheiro tem equipamento capaz de fazer este encurvamento de maneira fácil. Após encurvados os três tubos 3/8 de meio metro foram soldados ao cano de aço. As figuras 3b e 3c mostram a disposição dos tubos.
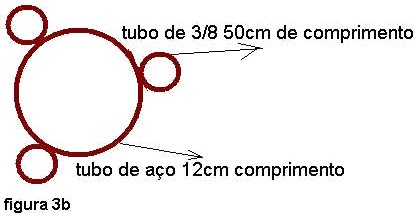
Quando voltei do serralheiro tinha o cano de aço preso a três tubos e o cubo soldado ao metalon.
O próximo passo foi prender o garfo ao cano de aço.
Antes de prender o garfo ao cano de aço com os três tubos já soldados, que chamarei de tripé, coloquei corretamente os primeiros acessórios do kit garfo.
O garfo tem a forma de Y, isto é, tem três segmentos. Primeiro deve-se colocar a arruela no segmento que segura as pontas, depois uma das aranhas com esferas, depois uma das bacias. Esta montagem deve permitir a livre rotação da bacia na junção entre as pontas do garfo e a base de sustentação.

Feito isto pude encaixar o tripé na montagem descrita anteriormente. Antes de completar a montagem garfo-tripé preenchi o espaço vazio entre a base do garfo e o cano do tripé com retalho. A tira de retalho utilizada tinha aproximadamente as dimensões 4cm por 3m. Não é importante que o retalho seja exatamente como foi sugerido, o importante é que preencha completamente o espaço vazio e fique bastante apertado neste espaço de modo a garantir um atrito estático quando não houver interferência intencional. O resultado é que depois de tudo montado a base ficou estável quando o telescópio foi apontado para um certo ponto. Distribuição irregular das massas do telescópio tendem a fazer o garfo girar dependendo da posição e do nivelamento em que se encontra o telescópio. O retalho com o atrito proporcionado irá evitar giros indesejáveis e ao mesmo tempo permitirá um giro intencional suave e estável. Então se o telescópio for apontado para Marte no horizonte, ou para a Lua no Zênite o telescópio não gira até que haja interferência intencional.
Encaixei a outra bacia do kit garfo, depois a aranha com as esferas, depois a porca que se enroscou à base do garfo e pressionou as esferas depois a arruela e finalmente a grande porca. O ajuste final destas porcas foi feito depois da montagem final do telescópio. Não precisei de nenhuma ferramenta para fazer esta montagem, pois não se deve apertar demais as porcas. Deve-se enroscá-las com as próprias mãos. Claro que para apertar os retalhos dentro do cano precisei utilizar uma haste de metal, mas qualquer outro instrumento que possa socar um retalho serve, como por exemplo uma chave de fenda.
O próximo passo foi aumentar as bases do tripé. Para isto utilizei as seis braçadeiras e os três tubos 3/8 de um metro de comprimento cada. Primeiro folguei as braçadeiras, ou seja, aumentei o tamanho de sua circunferência. Coloquei um tubo do tripé junto com um dos tubos de um metro e encaixei duas braçadeiras de modo que ficassem afastadas. Girei o parafuso de cada braçadeira com uma chave de fenda, até que os tubos ficaram firmemente presos. Repeti o procedimento para os outros tubos do tripé.
Faltava prender o metalon ao garfo. Primeiramente passei o eixo por dentro do cubo, depois coloquei as bacias de direção, uma em cada lado, depois as arruelas grandes. Este conjunto foi preso ao garfo de modo que as arruelas e bacias ficaram internamente. A figura 3d mostra o metalon com o cubo soldado no seu centro e acompanhado do eixo e seus acessórios.
Feito isto coloquei as pequenas arruelas uma de cada lado do eixo e depois enrosquei e apertei as porcas. O ajuste final das porcas foi feito depois da montagem final do telescópio. Não foi necessário ferramenta para apertar estas porcas. O ajuste final pode ser obtido utilizando as próprias mãos. A figura 3a mostra o resultado da montagem.
A idéia foi construir dois telescópios idênticos exceto pela distância focal da objetiva, no caso fob=2.000mm e fob=920mm e é claro o comprimento do tubo que cada um requer. O telescópio de 2.000mm é pesado e comprido de modo que o tripé é muito importante na sua utilização devido à maior capacidade de aumento. Já o telescópio de 920mm é menor leve, portátil , baixo custo e pode ser montado por qualquer pessoa sozinha ou com a orientação de alguém.
O que será exposto aqui sobre os telescópios é o resultado de muitos testes e experiências, os melhores resultados foram preservados. Dentro do prazo disponível busquei por melhores preços e melhores maneiras de se construir os telescópios e busquei também a máxima eficiência de funcionamento.
A procura por preços mais acessíveis exigiu de mim muita pesquisa e alguns itens foram difíceis de serem encontrados. Nos lugares que fui me perguntavam para que eram aquelas lentes, aqueles tubos e eu respondia a verdade e me lembro que quase todos que me atenderam ficaram curiosos e me pediram para mostrar os resultados depois. Dois atendentes disseram que tentaram construir uma luneta, mas não conseguiram, o motivo alegado era a falta de conhecimento básico de lentes.
| Quantidade | Materiais | Preço total mínimo(R$) |
|---|---|---|
| 2m | Tubo de PVC 2”. | 19,00 |
| 1 | Caps(tampão) 2” | 4,10 |
| 1 | Bucha de redução 2”x1 ½” | 3,70 |
| 1 | Bucha de redução 1 ½ “x ¾ “ | 2,50 |
| 17cm | Tubo de PVC ¾” | 0,50 |
| 1 | Luva de 2” | 5,00 |
| 2 | Luva de ¾ “ | 1,60 |
| 1 | Niple ¾” | 0,60 |
| 2 | Braçadeiras 64-76 | 2,60 |
| 2 | Anel de borracha 2” | 1,60 |
| 2 | Anel de borracha ¾” | 1,60 |
| 2 | Latinha de tinta preta fosca 112,5ml | 5,00 |
| 1 | Latinha de tinta esmalte 112,5ml para acabamento | 2,50 |
Os materiais listados na tabela 3b podem ser adquiridos em casas de materiais de construção ou casas de material hidráulico.
| Quantidade | Material ou serviço | Preço total mínimo(R$) | Onde encontrar |
|---|---|---|---|
| 1 | Lente +0,50 “grau” | 10,00 | Ótica |
| 2 | Lente +6,0 “graus” | 20,00 | Ótica |
| 2 | Lupa f=100mm | 10,00 | Papelaria |
| 1 | Capa preta para encadernação | 0,50 | Papelaria |
| ---- | Serviço do óptico | 10,00 | Óptica |
| ---- | Serviço do bombeiro | 3,00 | ---- |
| ---- | Serviço de torneiro | 2,00 | |
| ---- | Total tabelas 3b+3c | 105,80 | ------- |
Estes são os materiais e serviços que necessitei para a construção do telescópio de 2000mm. Explicarei cada item para ficar mais claro como foi a construção do telescópio.
A montagem do telescópio requer que os centros ópticos das lentes fiquem alinhados e que seus planos fiquem paralelos. O resultado é que os raios de luz que entram pela objetiva e saem pela ocular ficam colimados. Para isto foi necessário que o tubo fosse de 2” (lê-se duas polegadas). Este tubo é bastante rígido e se encurva muito pouco quando tem extensão de 2m, visto que o telescópio ficará sobre o metalon rígido o tubo praticamente não se encurva. Para prender os acessórios a este tubo precisei procurar um bombeiro para fazer as roscas no tubo. O bombeiro cobrou um real por rosca. Para evitar que luz refletida pela tubo chegasse às oculares ele foi enegrecido por dentro através da tinta preta fosca. Para obter um bom resultado deixei a tinta escorrer dentro do tubo e o girei rápido para que esta se espalhasse mais uniformemente no seu interior.
O caps de 2” também chamado tampão é um peça hidráulica que serviu para prender a lente objetiva ao tubo. Foi necessário levá-la a um torneiro mecânico para que fizesse a abertura o que custou um real.
A luva de 2” é a primeira peça a ser presa na extremidade do tubo que recebe as oculares. É uma peça em forma de cilindro que tem uma rosca interna e se encaixa de maneira perfeita ao tubo de 2” já com rosca. Na luva de 2” se encaixa a bucha de redução de 2” x 1 ½ “ que serve para reduzir o diâmetro útil de 2” para 1,5”, daí o nome bucha de redução. Na bucha de redução de 2” x 1 ½ “ se encaixa a bucha de redução de 1 ½” x ¾ “ que serve para reduzir o diâmetro utilizável para ¾ “. Visto que todas estas peças têm roscas apropriadas, feito estes encaixes eu tinha um tubo de 2” com um caps com uma abertura de 40mm. Preso ao tubo de PVC numa extremidade e uma abertura com rosca com ¾ “ na outra.
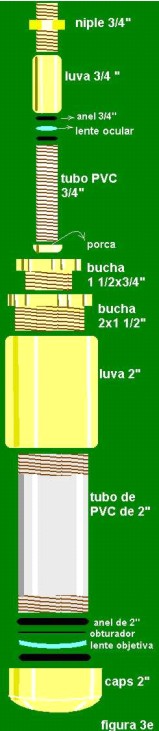

Cada lente ocular requer uma distância à lente objetiva de modo a resultar em imagem nítida. A solução encontrada foi pedir ao bombeiro que fizesse uma rosca no tubo de ¾” de comprimento 17cm. Este tubo também foi enegrecido por dentro e pôde se enroscar na bucha de redução 1 ½ x ¾ “ já que esta tem uma abertura de ¾ “. O bombeiro tinha sobras deste tubo e me cobrou R$0,50 pelo tubo e um real pela rosca.
A luva de ¾” é um cilindro com rosca interna que se encaixa em tubos com rosca de ¾”. Esta luva serve para acomodar as lentes oculares com seus anéis de borracha e prender tudo ao tubo de ¾” que pode se encaixar na bucha de redução já presa ao tubo de PVC de 2”.
A bucha de redução 1 ½ “ tem uma abertura que não permite a livre entrada do tubo de ¾” porque ela tem abertura com rosca um pouco afunilada. A solução foi pedir ao torneiro que retirasse o excesso, de modo que o tubo de ¾” pudesse entrar completamente. O problema é que a bucha de redução não foi feita para que um tubo percorra uma grande distância pela sua abertura, a bucha de redução é feita para que apenas alguns centímetros de tubo ou de niple possam passar. O torneiro cobrou um real por este serviço.
Os anéis de borracha servem para evitar o contato das lentes com os tubos e também para ajudar no alinhamento e também para evitar que a as forças que atuam na objetiva sejam não simétricas. No caso da objetiva coloquei um anel de borracha de 2” dentro do caps, depois a objetiva, depois um obturador de plástico, que explicarei posteriormente, depois outro anel de borracha de 2”, depois enrosquei o caps no tubo de PVC 2”.
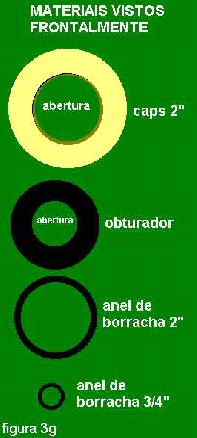
A capa preta para encadernação foi utilizada para confecção de círculos com aberturas que permitem ajustar a área da lente a ser utilizada. O motivo é que conforme a observação os efeitos da aberração esférica são mais acentuados e em outros este efeito não é tão importante. A figura 3g mostra o aspecto destes obtudaradores que têm aberturas de 20mm, 24mm, 25mm e 30 mm e sem obturador a abertura é a do caps 2” que é de 40mm.
Conforme já foi dito a(s) lente(s) oculares(s) se encaixam dentro da luva de ¾” com os anéis de borracha ¾”. Esta luva se encaixa no tubo ¾” e para que tudo fique bem firme na outra extremidade da luva é encaixado o niple ¾” que serve para prender as lentes oculares e também para servir de referência ao olho durante a observação. Quando o tubo ¾” foi encaixado na bucha de redução ficou um pouco folgado e os raios não ficavam colimados. A solução foi serrar aproximadamente 10mm da luva de ¾ “, estes 10mm de luva de ¾” serviram como porca para prender firmemente o tubo de ¾” à bucha de redução 1 ½ x ¾ “, o bombeiro não cobrou nada por isto já que ele já havia feito várias roscas.
Como oculares utilizei duas lupas e duas lentes de resina de 6,00 “graus” que na verdade são 6,00di. As lupas são muito grandes e apresentam aberração esférica muito intensa já que não foram projetadas para funcionar como oculares de telescópios o mesmo se aplica às lentes de resina. Então fui a um óptico para adquirir as lentes objetivas, oculares e pedir para que este cortasse as lupas de modo que estas pudessem se encaixar à luva de ¾” e ficando menores diminuíssem a aberração esférica que pude constar comparando a utilização das lupas antes e depois de serem cortadas.
O óptico cobrou cinco reais para cortar as duas lupas, isto aparece na tabela como 10,00 em serviço do óptico. Cada lente de resina ou de cristal custava R$7,00, mas por não se encaixarem no caps 2” ou na luva ¾” cada lente foi adquirida por R$ 10,00 sendo que o aumento no custo foi devido ao trabalho do óptico ao cortar estas lentes no tamanho adequando de modo a se encaixarem nos seus devidos lugares. Para chegar a este óptico eu tive de pesquisar bastante cheguei a encontrar as mesmas lentes por até R$ 30,00 cada uma fora o trabalho do óptico.
As figuras 3e,3f e 3g mostram em esquema as peças e a montagem do telescópio. Este tubo foi pintado com tinta esmalte Alumínio para dar um acabamento e adquirir uma aparência melhor. Claro que outras cores poderiam ser utilizadas o Alumínio foi um escolha minha.
Depois de montado o telescópio 2.000mm foi preso ao metalon através de duas braçadeiras 64-76. Na tabela 3b aparece a utilização de duas latinhas de tinta preta fosca é que uma das latas foi utilizada para dar acabamento ao tripé. A montagem final não necessitou de contra pesos e foi possível apontar para qualquer ponto do céu.
O telescópio 920mm é praticamente idêntico ao de 2.000mm. As próximas tabelas mostram o que foi necessário para sua construção.
| Quantidade | Material ou serviço | Preço total mínimo(R$) |
|---|---|---|
| 0,75m | Tubo de PVC 2”. | 9,50 |
| 1 | Caps(tampão) 2” | 4,10 |
| 1 | Bucha de redução 2”x1 ½” | 3,70 |
| 1 | Bucha de redução 1 ½ “x ¾ “ | 2,50 |
| 17cm | Tubo de PVC ¾” | 0,50 |
| 1 | Luva de 2” | 5,00 |
| 2 | Luva de ¾ “ | 1,60 |
| 1 | Niple ¾” | 0,60 |
| 2 | Anel de borracha 2” | 1,60 |
| 1 | Latinha de tinta preta fosca 112,5ml | 5,00 |
| 1 | Niple ¾” | 0,60 |
| 1 | Latinha de tinta esmalte 112,5ml para acabamento | 2,50 |
| Quantidade | Material ou serviço | Preço total mínimo(R$) | Onde encontrar |
|---|---|---|---|
| 1 | Lente +1,0 “graus” | 10,00 | Ótica |
| 2 | Lente +6,0 “graus” | 20,00 | Ótica |
| 2 | Lupa f=100mm | 10,00 | Papelaria |
| 1 | Capa preta para encadernação | 0,50 | Papelaria |
| ---- | Serviço do óptico | 10,00 | Óptica |
| ---- | Serviço do bombeiro | 3,00 | ---- |
| ---- | Serviço de torneiro | 2,00 | |
| ---- | Total tabelas 3b+3c | 93,70 | ------- |
Os materiais e serviços listados nas tabelas 3b e 3c são os mesmos das tabelas 3d e 3e e a descrição é a mesma já feita para o telescópio 2000mm. Tudo o que está formatado sem itálico e não sublinhando foi adquirido ou feito apenas uma vez e são comuns aos dois telescópios. Já o que está sublinhando e em itálico é específico de cada telescópio e foi adquirido individualmente.
Problemas na construção destes telescópios podem ocorrer se as lentes não apresentarem a distância focal indicada na compra. Eu tinha uma lente de 0,50di (meio "grau") que deveria resultar numa distância focal de 2m já que potencia=1/f se f é a distância focal em metros e que não apresentava f=2m, mas aproximadamente 1,80. A lente de 1,0di que deveria ter distância focal de 1,0m tinha na verdade uma distância focal de 920mm. A estratégia é verificar experimentalmente se a distância focal da lente é mesmo a obtida pela sua potência. Conforme já foi dito se um objeto está muito distante da lente sua imagem aparece no seu foco. Durante a noite a imagem da lâmpada de um poste distante pode ser projetada numa parede e com uma fita métrica pode se medir a verdadeira distância focal das objetivas e assim escolher o melhor tamanho para o tubo de PVC.
Os custos dos telescópios não ficaram tão baixos, mas devemos nos lembrar que só as oculares representam quase metade do custo no caso do telescópio de 2000mm e mais da metade do custo no caso do telescópio de 920mm. Quatro oculares dá a possibilidade de cinco combinações de associação: lupa + lupa, lupa + resina, resina + resina, lupa e resina. Um binóculo capaz de concorrer em qualidade de imagem com os telescópios construídos custam em torno de R$400,00. Instrumentos óticos com qualidade de imagem geralmente custam muito caro.
Este telescópio por ser um pouco pesado é melhor utilizado preso ao tripé. Este conjunto pode apontar para qualquer ponto do céu. Os movimentos são suaves e estáveis mas. Visto que as lentes utilizadas não são ideais para observações astronômicas dependendo da observação é necessário a utilização de obturadores que reduzem a região utilizada da lente objetiva diminuindo assim a aberração esférica. Para objetos muito brilhantes como a Lua o obturador de 20mm resulta em excelentes imagens onde praticamente se elimina a aberração cromática e esférica. Corpos com brilho maior permitem o uso de obturadores de menor diâmetro. A aberração cromática neste telescópio é pouco acentuada. Somente se o obturador tem diâmetro maior do que 30mm a aberração cromática prejudica bastante a imagem, principalmente se o corpo for muito brilhante.
As imagens obtidas são de boa qualidade, os objetos podem ser vistos nitidamente e o ajuste da nitidez é muito fácil graças ao tubo de ¾ " com rosca que permite a movimentação da lente ocular.
Realizei algumas experiências com o telescópio para determinar qual é a sua melhor resolução prática. Quando digo resolução prática quero me referir à resolução experimental, ou seja, a resolução em certas condições verificadas diretamente. O método utilizado para a obtenção da resolução prática é o seguinte: Procuro observar algum objeto em que eu tenha condições de determinar qual é o seu ângulo visual a olho nu e posteriormente verifico se este objeto ao ser visto através do telescópio está no limite da minha capacidade de resolvê-lo. Por exemplo eu não consigo reconhecer o rosto de uma pessoa localizada a 4Km de distância utilizando o telescópio, mas olhando com muita atenção consigo ver a forma de uma pilastra de concreto de aproximadamente 20cm de espessura quando iluminada pelo Sol. Esta pilastra serve para a determinação da resolução prática, pois seu ângulo visual vista pelo telescópio deve estar próxima da resolução do olho humano.
A resolução simples é o melhor resultado que pode ser obtido pois na sua determinação não se leva em conta efeitos como: absorção de luz pela atmosfera, absorção de luz pelas lentes, efeitos da difração que são inevitáveis, aberração esférica aberração cromática entre outros fatores. A resolução prática traz consigo o resultado de todos os efeitos negativos citados anteriormente e serve para se saber a real eficiência do telescópio.
Uma das experiências que fiz foi observar casas localizadas a 4.500m de distância da minha residência onde os 4.500m foram obtidos graças a um mapa da cidade com escala. Numa certa manhã quando o Sol iluminou uma janela cujo modelo era bem conhecido por mim. Pude ver uma das partes da mesma cujo comprimento era de 20cm. A identificação desta parte da janela foi feita no limite da minha capacidade de resolução e assim pude utilizar este experimento para determinar uma das resoluções práticas. A resolução prática é simplesmente o ângulo visual do objeto quando visto a olho nu. Neste caso o ângulo visual a olho nu foi de 0,2m/4500m=0,000044rad=9,16". Este resultado trouxe consigo os efeitos da turbulência atmosférica entre outros já citados anteriormente. Claro que a olho nu não pude ver nem sequer a janela, as dimensões de partes da janela e a distância foram obtidos indiretamente.
Outra tentativa foi observar o planeta Saturno no dia 16 de Janeiro de 2006. Nesta data este planeta estava praticamente em oposição e pude identificar a distância entre este e o início do anel B. A clara identificação desta distância no meu limite de resolução tornou possível a determinação de outra resolução prática. A distância entre a borda de Saturno e a borda interna do anel B é de 31.732Km. A distância entre Saturno e a Terra nesta experiência era de aproximadamente 1.276.000.000Km, então a resolução prática é: 31.732Km/1.276.000.000Km, que resulta em 0.0000248rad=5,12".
Estas experiências foram realizadas com o telescópio ampliando 40 vezes e a tabela 4b mostra que a resolução simples para este aumento é de 1,5". Os resultados experimentais foram bem piores mas serviram para dar noção da eficiência do telescópio.
As oculares podem ser associadas para formar uma lente de distância focal diferente. Utilizando a eq/1c e a relação potência=1/f se f em metros e potência em “graus” obtive a tabela 4a
| Lente(s) | Foc(mm) |
|---|---|
| Lupa + lupa | 50,0 |
| Lupa + resina | 62,5 |
| Resina + resina | 83,3 |
| Lupa | 100 |
| Resina | 166 |
Lupa + lupa significa a associação de uma lupa com outra. Resina se refere à lente ocular de resina listada nas tabelas da parte III. foc é a distância focal da ocular obtida com a associação ou a distância focal da lente simples.
| foc(mm) | Ampliação M | Rs (segundos) |
|---|---|---|
| 50 | 40 | 1,5 |
| 62,5 | 32 | 1,8 |
| 83,3 | 24 | 2,5 |
| 100 | 20 | 3,0 |
| 166 | 12 | 5,0 |
A ampliação M foi obtida utilizando a eq/2b e foc foi obtida na tabela 4a. A resolução simples abreviada como Rs foi obtida utilizando a eq/2e. A tabela 4b mostra as várias possibilidades de ampliação para o telescópio. As ampliações correspondem à realidade, mas a Rs conforme já foi dito é um valor obtido com idealizações. O valor Rs é simplesmente a resposta à pergunta: Qual o ângulo visual que multiplicado por M resulta em 60"? onde 60" é aproximadamente a resolução do olho humano. Se o telescópio fosse perfeito e não sofresse os efeitos da absorção de luz pelas lentes, reflexão da luz pelas lentes, absorção atmosférica, as lentes não apresentassem aberração esférica ou cromática entre outros fatores, Rs seria um valor real e verdadeiro. A tabela 4b mostra que Rs aumenta com a redução da ampliação. Isto fica evidente quando nos lembramos que se o telescópio amplia menos o ângulo mínimo que ele é capaz de nos permitir resolver aumenta. Quanto menor o aumento menos detalhes e pior é a resolução.
As primeiras observações que fiz foram observações terrestres. Pude ver com excelente nitidez casas e edifícios localizados a até 12Km de distância. Quando em boas condições atmosféricas era possível identificar pelo menos as janelas e portas das casas nesta distância. Constatei que a aberração cromática era imperceptível quando observava casas, ruas, pessoas, roupas no varal e tudo o mais que se pode ver na luz do dia. Se a ampliação M era modificada para valores maiores o brilho diminuía, mas a resolução ficava melhor, constatei que aumentos maiores do que 40 vezes não resultava em melhores resoluções, apenas a ampliação ficava aumentada.
A primeira observação astronômica que fiz foi observar a Lua na fase crescente e depois na quarto crescente. Como a Lua é muito brilhante utilizei o obturador de 20mm e as imagens foram excelentes. Pude ver grandes crateras e até pequenas crateras dentro de grandes crateras, pude ver diferenças de tonalidades na sua superfície, montanhas e sombras.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | d (Km) |
|---|---|---|---|---|
| 40 | 1,5 | 2,79 | 20,8 | 9.600 |
| 32 | 1,8 | 3,35 | 16,6 | 12.000 |
| 24 | 2,5 | 4,65 | 12,5 | 16.000 |
| 20 | 3,0 | 5,58 | 10,4 | 19.200 |
| 12 | 5,0 | 9,30 | 6,2 | 32.000 |
Tmin foi obtido através da eq/2f e representa o menor tamanho de um objeto na Lua que poderia ser resolvido utilizando o telescópio. Conforme já foi dito, os valores de Tmin estão limitados à determinação da resolução simples e traz consigo suas limitações. O angulo visual é o ângulo no qual a Lua foi vista através do telescópio, este valor foi obtido multiplicando-se o ângulo visual da Lua a olho nu que é de aproximadamente 0,52º, pela ampliação M. A distância “d” para a qual deveríamos ir para que o ângulo visual fosse o mostrado na tabela 4c foi obtido utilizando a eq/2c, d=D/M. A distância d representa a distância para qual o telescópio leva a nossa visão.
Outro astro que observei foi Júpiter. Não estava em oposição, mas havia pouco tempo que não estava mais, pois a observação foi realizada em Junho de 2005. Pude ver os satélites Galileanos e observar ao longo dos dias que mudavam de posição em relação ao planeta. Não pude ver as faixas equatoriais ou qualquer detalhe da sua superfície. Júpiter pareceu um círculo branco amarelado. Mas os satélites foram vistos de maneira bastante clara em todos os tipos de aumento.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | d (106 Km) |
|---|---|---|---|---|
| 40 | 1,5 | 4.806 | 0,49 | 16,52 |
| 32 | 1,8 | 5.768 | 0,39 | 20,65 |
| 24 | 2,5 | 8.011 | 0,29 | 27,54 |
| 20 | 3,0 | 9.613 | 0,24 | 33,05 |
| 12 | 5,0 | 16.023 | 0,14 | 55,08 |
A tabela 4d mostra algumas características das observações de Júpiter quando este estiver em oposição em 4 de Maio de 2006. Nesta data a distância à Terra será de 4,41269 UA. Os números da tabela foram obtidos utilizando esta distância e adotando como diâmetro de Júpiter 143.000Km. O valor 0,49º mostra que o ângulo visual mostra que Júpiter poderá ser visto quase do tamanho da Lua. Nas minhas observações não pude ver os detalhes de Júpiter como vejo os detalhes da Lua a olho nu, isto porque o fluxo na área "ao" da imagem na retina é menor do que aquele que eu teria se fosse para onde o telescópio levou minhas vistas na observação. Em outras palavras o ângulo visual é grande, mas o contraste não é bom o suficiente.
Os ângulos visuais obtidos para Júpiter só seriam possíveis a olho nu se nos deslocássemos para distâncias muito, mas muito além da órbita de Marte. Estaríamos muito mais próximos de Júpiter do que de Marte mesmo no caso em que a ampliação é de apenas 12 vezes.
No começo do ano observei o planeta Vênus com o telescópio e como este estava quase do outro lado do Sol eu o vi como um círculo muito brilhante e bastante pequeno.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | d (106 Km) |
|---|---|---|---|---|
| 40 | 1,5 | 729 | 0,27 | 2,50 |
| 32 | 1,8 | 875 | 0,22 | 3,13 |
| 24 | 2,5 | 1.216 | 0,16 | 4,18 |
| 20 | 3,0 | 1.460 | 0,14 | 5,01 |
| 12 | 5,0 | 2.432 | 0,08 | 8,36 |
A tabela 4e mostra características da observação de Vênus quando este estiver estacionário e começando a retornar para se aproximar do Sol, ou seja, Vênus na máxima distância angular ao Sol quando visto da Terra. Isto aconteceu no dia 23 de Dezembro de 2005. Neste dia sua distância à terra era de aproximadamente 100.360.000Km, O ângulo visual do seu diâmetro era de 24,86". As informações na tabela foram obtidos utilizando esta distância e adotando como diâmetro de Vênus 12.100 Km.
Eu tive a oportunidade de observar Vênus no final de novembro e foi possível constatar que sua forma lembrava a lua na fase quarto crescente ou quarto minguante. Com o telescópio foi realmente possível ver que Vênus apresenta fases.
Observei também o planeta Saturno com o telescópio. As observações foram feitas no começo do ano e este planeta estava praticamente do outro lado do Sol e o resultado das observações não foram muito bons. O que vi foi apenas uma figura meio amarelada. Conforme já citei observei Saturno também em Janeiro de 2006 e figura ao lado mostra aproximadamente o que vi.

A figura mostra apenas que não foi possível ver detalhes, mas foi possível identificar o espaço vazio entre os anéis e o planeta. Acho que a observação valeu a pena por eu ter conseguido ver este espaço vazio.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | d (106 Km) |
|---|---|---|---|---|
| 40 | 1,5 | 1.090 | 20,8 | 3,75 |
| 32 | 1,8 | 1.308 | 16,6 | 4,68 |
| 24 | 2,5 | 1.817 | 12,5 | 6,25 |
| 20 | 3,0 | 2.181 | 10,4 | 7,50 |
| 12 | 5,0 | 3.636 | 6,2 | 12,5 |
A tabela 4f mostra alguns dados sobre a observação do Sol. Um fato interessante é d = 3.750.000 Km. A imagem do Sol que veria teria o mesmo tamanho que se eu me afastasse da Terra de 146.250.000 Km em direção ao Sol. É uma viagem de milhões de Km apenas trocando de ocular. Observei também o planeta Marte no começo de novembro de 2005. Não pude identificar detalhes da superfície. Vi este planeta apenas como um círculo avermelhado. Este planeta por apresentar um diâmetro muito pequeno dificulta observações de detalhes utilizando telescópios não profissionais. A tabela 4g mostra alguns dados sobre as observações de Marte quando este estive em oposição no dia 7 de Novembro de 2005 e a uma distância de 69.610.500 Km da Terra.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | d (106 Km) |
|---|---|---|---|---|
| 40 | 1,5 | 506 | 0,22 | 1,74 |
| 32 | 1,8 | 532 | 0,18 | 2,17 |
| 24 | 2,5 | 738 | 0,13 | 2,90 |
| 20 | 3,0 | 1.012 | 0,11 | 3,48 |
| 12 | 5,0 | 1.687 | 0,07 | 5,80 |
As observações que fiz têm características próximas às que aparecem na tabela pois quando realizei as observações Marte estava praticamente em oposição.
Não pude ver estrelas não visíveis a olho nu da Via-Láctea porque o céu de Belo Horizonte é muito claro durante a noite por causa das luzes da cidade, mas na constelação de Escorpião cheguei a ver muitas estrelas que não são visíveis a olho nu.
Este telescópio utiliza as mesmas oculares do telescópio de 2.000mm, exceto pela lente de resina sozinha. O motivo é que a lente de resina sozinha resulta em um aumento muito reduzido e requer que o tubo ¾" seja maior prejudicando as observações. Este telescópio tem uma distância focal menor e menores aumentos são obtidos. Como não utilizei tripé para realizar as observações as dificuldades de observação foram grandes porque por mais que tentasse ficar quieto não conseguia, e o astro nunca ficava totalmente parado durante a observação. As próximas tabelas mostram as características deste telescópio e das observações realizadas ou das possíveis observações.
| Foc(mm) | Ampliação M | Rs (Seg de arco) |
|---|---|---|
| 50 | 18,4 | 3,2 |
| 62,5 | 14,7 | 4,1 |
| 83,3 | 11,0 | 5,4 |
| 100 | 9,20 | 6,5 |
Estes são os dados para as observações realizadas para o Sol com este telescópio.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | D (106 Km) |
|---|---|---|---|---|
| 18,4 | 3,2 | 2.327 | 9,67 | 8,15 |
| 14,7 | 4,1 | 2.981 | 7,64 | 10,2 |
| 11,0 | 5,4 | 3.927 | 5,72 | 3,6 |
| 9,20 | 6,5 | 4.727 | 4,78 | 6,3 |
A tabela 4j mostra os dados para as observações da Lua.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | D (em Km) |
|---|---|---|---|---|
| 18,4 | 3,2 | 5,95 | 9,67 | 20.645 |
| 14,7 | 4,1 | 7,63 | 7,64 | 26.122 |
| 11,0 | 5,4 | 10,0 | 5,72 | 34.909 |
| 9,20 | 6,5 | 12,1 | 4,78 | 41.739 |
O que vi com este telescópio foi quase o mesmo que vi com o telescópio de 2.000mm, a diferença é que os aumentos são menores e portanto a Lua pareceu mais brilhante.
Observar Marte com este telescópio somente para ver que este planeta tem uma forma esférica, não consegui ver detalhes deste planeta mesmo este estando em oposição. A tabela 4k mostra as características da observação quando Marte em oposição no dia 7 de Novembro de 2005, a 69.610.500 Km distante da Terra e um ângulo visual a olho nu de 20,17" de arco.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | D (10 6Km) |
|---|---|---|---|---|
| 18,4 | 3,2 | 1.080 | 6,25 | 3,74 |
| 14,7 | 4,1 | 1.383 | 4,94 | 4,73 |
| 11,0 | 5,4 | 1.822 | 3,69 | 6,33 |
| 9,20 | 6,5 | 3.105 | 3,09 | 7,57 |
As observações de Júpiter foram mais interessantes porque foi possível ver os satélites e a mudança posicional que ocorria dia a dia. Estas observações foram feitas no mesmo período que fiz com o telescópio 2000mm. A tabela 4l mostra algumas características da observação quando Júpiter esteve em oposição no dia 3 de Abril de 2005, quando sua distância à Terra era de 668.496.000 Km e com ângulo visual a olho nu igual a 44,19" de arco.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | D (10 6Km) |
|---|---|---|---|---|
| 18,4 | 3,2 | 10.371 | 0,23 | 35,94 |
| 14,7 | 4,1 | 13.288 | 0,18 | 45,47 |
| 11,0 | 5,4 | 17.501 | 0,13 | 60,77 |
| 9,20 | 6,5 | 21.066 | 0,11 | 72,66 |
Observei Saturno com este Telescópio e também consegui ver aproximadamente o que relatei para o telescópio 2000 mm, mas a identificação foi bastante precária de modo que somente no aumento máximo pude ver o espaço vazio entre o planeta e os anéis.
Observei também o planeta Vênus com este telescópio no final de Novembro e pude vê-lo praticamente na forma da Lua quarto crescente ou quarto minguante. No dia 23 de Dezembro de 2005 este planeta estará no máximo afastamento angular do Sol visto da Terra. Neste dia seu ângulo visual a olho nu será de 24,86" de arco e sua distância à Terra será de 100.360.000 Km. A tabela 4m mostra os dados para as possíveis observações deste planeta neste dia.
| Ampliação M | Rs (s de arco) | Tmin (Km) | Ângulo visual (graus) | D (10 6Km) |
|---|---|---|---|---|
| 18,4 | 3,2 | 1.556 | 7,62 | 5,45 |
| 14,7 | 4,1 | 1.995 | 6,09 | 6,82 |
| 11,0 | 5,4 | 2.627 | 4,55 | 9,12 |
| 9,20 | 6,5 | 3.162 | 3,81 | 10,9 |
Realizei muitas observações terrestres com este telescópio e o que mais me chamou a atenção é que praticamente não havia aberração cromática quando utilizei o obturador de 20mm. Uma dos fatos que mais me chamou a atenção foi a capacidade de poder identificar com clareza janelas de prédios localizados a mais de 15 Km de distância quando em boas condições atmosféricas.
Este telescópio é interessante por ser portátil, muito leve e curto. Com pequenos aumentos os resultados das observações não são muito interessantes. Os melhores resultados foram obtidos utilizando a ampliação máxima que é M= 18,4. Penso não ser útil o uso de outras combinações de oculares.
Conforme vimos nas descrições das características dos telescópios, eles apresentam várias possibilidades de utilização e podem proporcionar observações de excelente qualidade dependendo do astro.
No ensino fundamental é ensinado aos jovens muito sobre Ciência. Eles aprendem Biologia, Geografia, Um pouco de Física e Química. É no ensino fundamental que pela primeira vez aprendem sobre onde estamos aqui na Terra, onde se encontra a Terra no Sistema Solar e assim por diante.
No ensino fundamental os jovens aprendem que o Sistema Solar tem nove planetas, que a Terra é o terceiro, aprendem os tamanhos relativos dos planetas, aprendem um pouco sobre a Lua o Sol e as estrelas.
O ensino de Ciências no ensino fundamental é fortemente baseado na descrição e os jovens ficam um pouco passivos em relação às ações no processo ensino aprendizagem.
Mas nesta fase da vida os jovens estudantes são muito mais curiosos que nas outras fases. Os jovens do ensino fundamental ficam muito encantados com novidades e experiências que mostram na prática o que foi aprendido chama muito a atenção. É como se encontrassem com alguém que conhecem da televisão.
Durante a vida inteira ouve-se falar em Lua, Sol, Mercúrio, anéis de Saturno, etc. Mas a grande maioria nunca viu sequer a olho nu, sabendo do que se tratava, um planeta como Júpiter ou Vênus. Ver astros a olho nu já desperta curiosidade principalmente nos jovens que certamente conhecem estes astros dos filmes, desenhos animados, etc. Tive a oportunidade de mostrar a alguns jovens da quinta a oitava série o planeta Marte e Vênus, eles ficaram admirados e todos eles achavam que a olho nu isto não era possível. Não houve exceção na demonstração de curiosidade diante do fato novo. Quando mostrei Vênus disseram: "mas aquilo é uma estrela".
Imaginemos como se comportariam estes jovens ao verem com os próprios olhos as crateras e montanhas da Lua, ver Saturno, fases de Vênus. Será uma experiência inesquecível para os que nunca tiveram a oportunidade de olhar os astros sequer com um binóculo que aumenta dez vezes e com má qualidade.
Acreditamos que será muito proveitoso para os professores em geral a inclusão de atividades extra-classe com utilização dos telescópios.
Durante as aulas de Ciências quando se estiver falando de modelos de Universo, ou quando se estiver descrevendo o Sistema Solar será muito útil a inclusão de observações de alguns astros do Sistema Solar para que as informações passadas pelo professor e as discussões se tornem muito mais reais para os alunos. As observações com o telescópio e a apresentação dos seus componentes, irá desmistificar o telescópio e os astros observados. Estes alunos deixarão de pensar que ver planetas como os próprios olhos é exclusivo de cientistas ou de pessoas de alto poder aquisitivo, poderão ver que um telescópio pode ser feito por eles mesmos ou com a ajuda de um adulto conforme a idade.
A proposta aqui é que os professores incluam na medida do possível, atividades extra-classe com os telescópios para mostrar: as crateras da Lua e montanhas da Lua, as luas de Júpiter, mostrar Saturno, as fases de Vênus, a Via-Láctea e estrelas que não são visíveis a olho nu. Marte achamos que vale a pena mostrar pelo menos sua forma arredondada.
O número de observações e o que deve ser observado deve ser adequado aos horários disponíveis pelos professores. Mas tenho certeza que os alunos ficarão muito interessados em ver os astros através dos telescópios. Numa cidade grande como Belo Horizonte as condições atmosféricas não são muito favoráveis para certas observações como por exemplo a Via-Láctea, mas os telescópios que construí dão excelentes condições de se observar, mesmo com o céu brilhando, por causa das luzes da cidade, as principais características dos astros que nos referimos anteriormente.
No Ensino Médio a descrição dos fatos históricos, científicos, etc., continuam, mas o amadurecimento dos alunos leva a uma interação muito mais ativa com o conhecimento. É esperado dos alunos do Ensino Médio a assimilação do conhecimento e a aplicação deste nas suas vidas. Espera-se destes alunos que a partir de receberem informações básicas sejam capazes de deduzir por conta própria muitas outras informações, que sejam capazes de prever ou explicar o que não está explicitamente escrito nos livros ou foi dito pelo professor.
No ensino de Física esta necessidade de autonomia dos alunos está muito mais presente. A partir do ensino de leis básicas, a apresentação de alguns exemplos e algumas demonstrações já é esperado que os alunos sejam capazes de entender uma enorme variedade de fenômenos naturais. Neste contexto os telescópios podem ser utilizados para auxiliar no aprendizado de Astronomia. Mas não só Astronomia mas também Física e a evolução das idéias com a própria construção dos telescópios.
No primeiro ano é ensinado em Física: movimento circular uniforme, leis de Newton, Gravitação Universal entre muitos outros assuntos. Quando é ensinado movimento circular uniforme na Segunda Lei de Newton e na Gravitação Universal o tema luas de Júpiter é de excelente abordagem, Visto que os Satélites Galileanos mudando de posição dia a dia será de muito proveito para auxiliar no entendimento de quase todo o conteúdo do primeiro ano. Os alunos do primeiro ano do Ensino Médio se queixam muito de que Gravitação Universal é muito abstrata e distante de suas realidades. A elaboração de um roteiro onde os alunos tenham a oportunidade de ver os planetas do Sistema Solar tornará muito mais real e interessante estes assuntos que são menosprezados pela maioria dos alunos do primeiro ano. Não se deve perder a oportunidade de contar sobre Galileu e a importância de suas observações.
No segundo ano é ensinado óptica e a construção dos telescópios é uma boa oportunidade para colocar em prática muito do que os alunos aprendem na teoria. É neste ano que a construção dos telescópios e sua utilização é mais útil e pode-se gastar mais tempo discutindo e aprendendo sobre eles.
O primeiro auxílio dos telescópios pode começar quando se ensinar sobre refração e lentes. Mostrar as lentes trabalhando para gerar imagens inacessíveis a olho nu dará às lentes maior importância na mente dos alunos. As lentes deixam de ser apenas desenhos com bordas grossas ou finas e que mostram a luz desviando apenas num plano. A maturidade maior facilita ao professor a encorajar estes alunos a construírem seus próprios telescópios.
A aberração cromática e esférica, os indesejáveis efeitos da difração também podem ser abordados em conjunto com a teoria e a prática na utilização dos instrumentos.
Claro que a utilização dos telescópios no ensino de Física no segundo ano não deve ficar restrito à óptica, mas deve-se também utilizá-los em observações terrestres e também astronômicas. Aqui as observações terrestres ganham importância por causa da abordagem teórica das lentes e dos próprios telescópios refratores.
No terceiro ano é ensinado em Física eletromagnetismo e Física Moderna. Aqui os telescópios podem aparecer como complemento no ensino de história da Ciência. É importante notar que certamente haverão muitos estudantes do terceiro ano que nunca utilizaram uma luneta ou telescópio. Este é para a grande maioria dos alunos de escolas públicas o último ano de estudos e o fim da carreira escolar. Talvez a novidade leve muitos a querer continuar a estudar.
Os alunos do terceiro ano em sua maioria sentem que o que aprenderam na escola não produziu quase nada que resultasse em aplicação prática. Sentem como se tudo o que viram serviu apenas para fazer provas. Os telescópios e as aulas sobre Astronomia podem reverter esta sensação e mostrar que o conhecimento muda o mundo e que estes alunos com conhecimento podem ser atores na transformação do mundo.
Acredito que vale a pena a união de forças nas escolas públicas que não possuem telescópios para a construção do telescópio de 2000mm. Não somente pelas possibilidades de utilização mas também pelo prazer e repercussão da construção. A construção poderia ter a participação de várias pessoas e os alunos veriam a evolução dos acontecimentos.
Acredito também que os professores devem encorajar os alunos a construírem para si mesmos um telescópio de lente de 1,00di, utilizando como ocular apenas a associação lupa+lupa o que resultará em um custo máximo de R$63,70. As imagens obtidas com este telescópio são muito boas nestas condições.
Galileu Galilei foi um cientista italiano que viveu de 1564 a 1642 e que tem grandes contribuições para a Física, Astronomia e Filosofia. Cientistas de nossa época o chamam de pai da Ciência moderna. Viveu numa época de transição entre ciência antiga e a moderna e foi um dos agentes que impulsionou esta transição, exercendo influência em consagrados cientistas como Isaac Newton, entre outros.
Na época de Galileu o modelo Geocêntrico vinha sofrendo questionamentos apesar de explicar satisfatoriamente bem nas circunstâncias da época, quase todos os aspectos do movimento dos corpos celestes. O modelo Geocêntrico afirmava que a Terra era estática e que todos os corpos celestes giravam em torno de um certo ponto próximo à Terra. Para explicar todos os aspectos dos movimentos dos planetas eram necessários complicados cálculos e complicadas órbitas. Uma das complicações era por exemplo o fato de Mercúrio e Vênus ficarem a maior parte do tempo próximos ao Sol no céu. Mercúrio nunca pode ser visto depois que se passaram uma hora e meia que o Sol se pôs. Vênus nunca pode ser visto depois que se passaram três horas e 8 minutos que o Sol se pôs. Outra complicação era o fato de os planetas Marte, Júpiter e Saturno se moverem em relação às estrelas fixas num sentido numa certa época e gradualmente diminuindo a velocidade até parar e começar a se mover em relação às estrelas fixas no sentido oposto. O modelo geocêntrico de Ptolomeu explicava estes fatos e tinha resultados quantitativos satisfatórios mas às custas de complexos cálculos e trajetórias para o movimento dos corpos celestes. O modelo de Ptolomeu era tão bom que era possível se fazer vários previsões em relação à posição dos corpos celestes no céu.
Em tempos muito antigos próximos ao início da Era Cristã já haviam propostas de um modelo Heliocêntrico, mas os argumentos ou não são muito bem conhecidos ou não eram muito plausíveis. Mas Nicolau Copérnico (1473-1543) propôs este modelo mostrando que todos os aspectos do movimento dos corpos celestes ficava extremamente mais simples de serem explicados supondo que os planetas se moviam em torno do Sol, inclusive a Terra que passava a ser mais um corpo celeste. A transição do modelo Geocêntrico para o Heliocêntrico foi difícil, pois não se sabia muito de Física nesta época e imaginar a Terra, em movimento e os corpos sobre ela não sendo expulsos dela era incompreensível para as pessoas desta época. Apesar de explicar de maneira muito simples os aspectos intrigantes do movimento dos planetas o modelo Heliocêntrico carecia de provas e ainda tinha estes aparentes desacordos com as leis da natureza.
Galileu ao ter notícia de um instrumento óptico que foi inventado na Holanda e que servia para que as óperas fossem vistas com mais detalhes, o adquiriu e o aperfeiçoou para observar o céu. Galileu foi o primeiro a utilizar a luneta para observar os corpos celestes.
A princípio construiu uma luneta que aumentava oito vezes e depois chegou a uma que aumentava vinte vezes.
As observações de Galileu derrubaram muitas afirmativas do modelo Geocêntrico e reforçou o modelo Heliocêntrico sem porém dar uma prova definitiva.
Ao observar a Lua, Galileu pôde ver suas crateras, montanhas e vales o que sugeria que sua estrutura era muito semelhante à da Terra, derrubando assim a tese de Aristóteles de que a Lua seria uma esfera lisa e perfeita. Ele foi o primeiro homem a ver certos detalhes da Lua.
Ao apontar sua luneta para Júpiter, Galileu pôde ver quatro corpos que se movimentavam próximos ao planeta sugerindo que estes estavam em órbita em torno do planeta assim como a Lua está em órbita ao redor da Terra. As quatro maiores luas de Júpiter foram descobertas por Galileu no ano de 1610. Hoje estas luas são muitas vezes referidas como Galileanas em homenagem ao cientista.
As quatro luas são Io que tem um período de revolução de um dia e dezoito horas, Europa que tem um período de três dias e treze horas, Ganymede que tem um período de sete dias e três horas e Calixto que tem um período de dezesseis dias e dezesseis horas. Estes períodos curtos facilitam a observação do movimento destes astros.
Como na época de Galileu não haviam relógios de precisão que poderiam funcionar em alto-mar não era possível determinar a longitude de um certo lugar. Galileu sugeriu então que as luas de Júpiter servissem como referência para um tempo universal que poderia servir de informação para se determinar a longitude de um certo ponto da Terra. Após a sua morte a idéia foi desenvolvida e foi utilizada por navegadores. A idéia é a seguinte: Sabendo-se que a Terra é esférica e que a cada quinze graus de longitude resulta numa diferença de uma hora, escolhe-se um local para ser o meridiano de zero grau de longitude, a determinação da longitude pode ser feita conhecendo-se a diferença de horário entre as duas localidades, o pôr-do-Sol por exemplo pode servir para marcar a hora local, no caso dezoito horas, a hora da localidade a zero grau pode ser determinada com um relógio ajustado lá, assim tem-se a diferença de horários. Como Júpiter poderia ser visto no mundo inteiro suas luas poderiam ser usadas como relógio comum e serviria para determinar a diferença de horários entre a referência e o local com a longitude a ser determinada.
As luas de Júpiter derrubavam a tese do modelo Geocêntrico de que todos os corpos giravam ao redor da Terra e causou grande indignação entre religiosos e defensores do modelo, pois a descoberta de mais quatro corpos celestes quebrava o número considerado mágico, no caso o número sete que é o número que se obtém ao contar os planetas visíveis a olho nu na época mais o Sol e a Lua. Onze corpos celestes deixava sem credibilidade as idéias que tinham por base o número sete para a explicação.
Ao apontar seu telescópio para Vênus Galileu pôde ver que este apresentava fases como a nossa Lua. Constatou também que Vênus parecia menor quando na fase cheio em analogia com a Lua Cheia, e que parecia maior quando na fase minguante ou crescente. Combinando a observação da evolução das fases de Vênus, o tamanho aparente, a mudança de brilho, e a possibilidade de se ver todas as fases não deixava dúvidas de que Vênus girava em torno do Sol e poderia estar do outro lado do Sol quando na fase cheio e entre a Terra e o Sol quando na fase minguante ou crescente.
Segundo o modelo Geocêntrico de Ptolomeu Vênus estava entre a Terra e o Sol e assim sendo só poderia apresentar fases crescentes minguantes e nunca as fases quarto crescente, quarto minguante ou cheio. As observações de Galileu não confirmaram estas previsões ao mostrar que Vênus poderia apresentar todas as fases.
Combinando o que foi dito sobre as fases de Vênus com o fato de este planeta estar a maior parte do tempo próximo ao Sol reforça fortemente a idéia de que este astro gira em torno do Sol e dá grande credibilidade ao modelo Heliocêntrico. Esta não é uma prova definitiva do modelo Heliocêntrico, e não prova que todos os planetas giram ao redor do Sol, mas ao derrubar teses do modelo Geocêntrico reforça o Heliocêntrico levando outros cientistas a procurar a prova definitiva que veio alguns séculos depois.
Galileu observou as manchas solares o que provocou também a ira da Igreja Romana que considerava perfeitos e imutáveis os corpos celestes.
A luneta de Galileu não era de boa qualidade como as de hoje, devido à dificuldade de se manipular o vidro para a confecção das lentes. Mas ele chegou a observar os anéis de Saturno sem no entanto entender o que realmente via, chegou a dizer que se tratavam de três corpos, ou que Saturno parecia ter orelhas, quando a Terra e os anéis ficaram num mesmo plano e ficaram invisíveis Galileu ficou confuso e não chegou a conclusões.
Desenhos de Galileu estudados atualmente mostram que ele observou o planeta Netuno que estava quase alinhado com Júpiter no céu. Como este planeta tem um longo período de translação e na época das observações estava praticamente imóvel em relação às estrelas fixas não pôde ser identificado como um planeta por Galileu. Nos desenhos dele Netuno aparece apenas como mais uma estrela fixa e não é creditada a ele a descoberta que foi concretizada em 1846 já utilizando Mecânica Newtoniana por Le Varrier.
Galileu mostrou também que a Via-Láctea não era contínua, mas sim composta de várias estrelas. Ele mostrou que o fato de a vermos como uma mancha branca era devido a incapacidade de a olho nu ver detalhes de sua constituição. Com sua luneta ele pôde ver que a Via-Láctea tinha pelo menos aglomerados de estrelas.
Galileu teve também contribuições para a Física, Matemática e tecnologia de canhões.
Um dos fatos mais marcantes na vida de Galileu foi a perseguição sofrida por ele por parte da Igreja Católica através do tribunal da inquisição. O motivo eram suas descobertas e suas idéias que entravam em choque com os interesses da Igreja ao tirar o privilégio da Terra defendendo um modelo que não tinha o nosso planeta como o lugar onde tudo deveria girar ao redor, classificava a Terra como mais um corpo celeste ao girar ao redor do Sol como os outros. Para se livrar da condenação teve de negar publicamente suas idéias. Mas os acontecimentos futuros não muito distantes da sua morte acabaram confirmando as idéias que ele ajudou a provar pelo menos em parte. Hoje tem seu lugar de reconhecimento e é lembrado com admiração por todos, principalmente pelos jovens que estudam parte de suas idéias no ensino fundamental na disciplina Ciências.
Comecei este trabalho falando do interesse das pessoas em Ciência. O objetivo principal deste trabalho foi chegar a um instrumento capaz de levar às pessoas sejam elas estudantes ou não uma opção barata de conhecer melhor a Astronomia. Falei sobre as contribuições de Galileu Galilei. Mostrei como suas investigações levaram a profundas mudanças no pensamento da humanidade. Mostrei como uma simples associação de lentes de vidro e curiosidade poderiam resultar em revoluções no caso realizadas por Galileu. Então mostrei em detalhes a construção dos telescópios fob=2000mm e fob=920mm. Expliquei o mais claro possível para que no caso de alguém se interessar em reproduzir o que fiz ter uma referência. Mostrei também os resultados das observações que realizei sendo que o foco foram as observações de Galileu Galilei. Finalmente fiz propostas de utilização e mostrando que o emprego de telescópios em escolas pode ser um estímulo para aproximar os alunos da Ciência e principalmente da Astronomia e Física.
Gostaria de expor muito mais sobre os telescópios e as observações, mas infelizmente no tempo que tive nem sempre tive boas condições atmosféricas ou astros em situações boas de observação. Mas penso que o que foi exposto aqui serve como referência para outras pessoas.
Quero relatar aqui alguns fatos que me aconteceram durante a construção dos telescópios. Um dos fatos mais marcante que me lembro foi quando fui a uma rua alta para fazer observações terrestres. Em poucos minutos estava cercado de curiosos que queriam ver também. O jovens que se aproximaram eram moradores de periferia e ficaram impressionados com os aumentos que o telescópio proporcionava, olharam para os prédios e placas no centro da cidade, olharam para a Serra do Curral e viram detalhes das torres de telecomunicação. Tive dificuldades para ir embora porque uma fila estava se formando para olhar pelo telescópio.
Os meus vizinhos me chamavam de professor Pardal e zombavam do meu sacrifício para observar os astros. Diziam: “Esta gambiarra não funciona”. Mas quando os convidei para ver a Lua e ruas a quilômetros de distância ficaram muito interessados e alguns amigos até começaram a construção de um telescópio semelhante aos que construí e me pediram dicas.
Quando fui comprar os materiais utilizados os vendedores me perguntavam para que era e eu respondia a verdade e eles ficavam ao mesmo tempo com cara de desconfiados, mas também muito curiosos e querendo ver os resultados.
Acabei percebendo na construção destes telescópios que as pessoas moradoras de periferia são muito curiosas quando o assunto se trata de telescópios e Astronomia. Por isto acredito que a presença de um instrumento deste numa escola pública onde os alunos nunca nem sequer viram de perto um telescópio terá excelente repercussão. Insisto que penso que a Astronomia é o caminho mais curto e agradável para levar jovens carentes ao encontro do conhecimento e os telescópios são ferramentas possíveis.
Astronomia é tão interessante que quando comecei a construir telescópios em 2003 acabei direcionando meu curso para Astrofísica. Enfim digo que aprendi muito com o trabalho que realizei juntamente com o professor Renato Las Casas. Considero muito proveitoso tudo o que fiz e aprendi.
Endereços eletrônicos: